
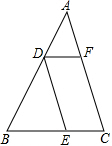
 如图,在锐角三角形纸片ABC中,AC>BC,点D,E,F分别在边AB,BC,CA上,已知:DE∥AC,DF∥BC.
如图,在锐角三角形纸片ABC中,AC>BC,点D,E,F分别在边AB,BC,CA上,已知:DE∥AC,DF∥BC.分析 (1)根据两组对边分别平行的四边形是平行四边形,即可解答;
(2)连接CD与EF相交于点O,根据平行四边形的对角线互相平分,O为CD的中点,再根据等腰三角形的性质(三线合一),连接BO,BO即为∠ABC的角平分线;
(3)根据△ADF∽△ABC推出对应边的相似比,然后进行转换,即可得出高h与x之间的函数关系式,根据平行四边形的面积公式,很容易得出面积S关于h的二次函数表达式,求出顶点坐标,就可得出面积s最大时h的值.
解答 解:(1)∵DE∥AC,DF∥BC,
∴四边形DECF是平行四边形.
(2)如图1,
连接CD与EF相交于点O,连接BO,BO即为∠ABC的角平分线,
理由:∵四边形DECF是平行四边形,
∴O是DC中点,
又∵DB=CB,
∴BO就是∠ABC的平分线;
(3)作AG⊥BC,交BC于G,交DF于H,如图2,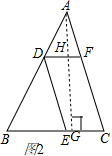
∵∠ACB=60°,AC=6cm
∴AG=AC•sin60°=$6×\frac{\sqrt{3}}{3}=2\sqrt{3}$,
设DF=EC=x,平行四边形的高为h,则AH=3$\sqrt{3}$-h,
∵DF∥BC,
∴△ADF∽△ABC,
∴$\frac{DF}{BC}=\frac{AH}{AG}$,
∴$\frac{x}{4}=\frac{3\sqrt{3}-h}{3\sqrt{3}}$,
∴x=$4(1-\frac{h}{3\sqrt{3}})$,
∵S=xh=4h-$\frac{4}{3\sqrt{3}}{h}^{2}$,
∴h=-$\frac{b}{2a}=-\frac{4}{2(-\frac{4}{3\sqrt{3}})}=\frac{3\sqrt{3}}{2}$,
∵AH=3$\sqrt{3}$,
∴AF=FC,
∴在AC中点处剪四边形DECF,能使它的面积最大.
点评 本题考查了相似三角形的判定及性质、二次函数的最值,关键在于根据相似三角形及已知条件求出相关线段的表达式,求出二次函数表达式,即可求出结论.


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:解答题
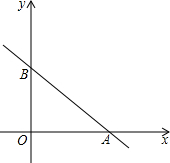 在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.求函数y=-$\frac{3}{4}$x+3的坐标三角形的三条边长.
在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.求函数y=-$\frac{3}{4}$x+3的坐标三角形的三条边长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 加号 | B. | 减号 | C. | 乘号 | D. | 除号 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com