
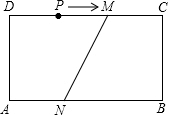
 ��ͼ������ABCD�У�AB=12cm��BC=4cm��DM=8cm��AN=5cm����P��CD���ϣ�
��ͼ������ABCD�У�AB=12cm��BC=4cm��DM=8cm��AN=5cm����P��CD���ϣ����� ��1����Ϊ�ı���ABCDΪ���Σ����A=��B=90�㣬���Ե�Pһ����D�غϣ�һ����C�غϣ�����������AB������APB=90�㣬ͨ��֤����AEP�ס�PEB������ȷ��P��λ�ã�����һ���з���������P��4����
��2������ֱ��l����һ����������λ���ϣ�����������H�㣬���ɡ�HNM=��HMN=90�㣻��MNΪֱ����һ����ԲO����Ϊֱ�����Ե�Բ�ܽ�Ϊֱ�ǣ��������ȼ��㵱ֱ��l��ԲO����ʱ��PD�ij����ȼ���FN=1�����Դ�ʱPD=5-1=4����ͼ4����˿��Է�Ϊ���¼���������ۣ�
��0��t��4ʱ����ͼ5����2��H�㣻 ��t=4ʱ����ͼ6����3��H�㣻��4��t��5ʱ����ͼ7����4��H�㣻 ��t=5ʱ����ͼ8����2��H�㣻��5��t��8ʱ����ͼ9����4��H�㣻
��t=8ʱ����ͼ10����2��H�㣮
��� �⣺��1������ͼ1������PAB=90��ʱ��P��D�غϣ�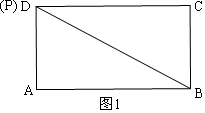
����ͼ2������PBA=90��ʱ��P��C�غϣ�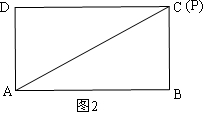
����ͼ3������APB=90��ʱ����P��PE��AB��E����PE=BC=4��
��PD=x����AE=x��EB=12-x��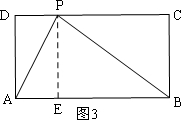
�ߡ�APB=90�㣬
���APE+��BPE=90�㣬
�ߡ�AEP=��PEB=90�㣬
���APE+��PAB=90�㣬
���BPE=��PAB��
���AEP�ס�PEB��
��$\frac{AE}{PE}=\frac{PE}{EB}$��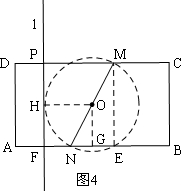
��42=x��12-x����
x=6$��2\sqrt{5}$��
����PD=6$+2\sqrt{5}$��6-2$\sqrt{5}$ʱ�����APB=90�㣬
��ʱ�����������������ĵ�P��
���������������P�����A��B����һ��ֱ�������Σ��������ĵ�P��4����
�ʴ�Ϊ��4��
��2����ͼ4����MNΪֱ����ԲO����ֱ��lΪ��O������ʱ�����е�ΪH������OH�����O��AB����һ������ΪE������ME��
��O��OG��AB��G��
��MN�ǡ�O��ֱ����
���MEN=90�㣬
��l��BC��
��l��CD��l��AB��
���CPF=��PFE=90�㣬
���ı���PFEM�Ǿ��Σ�
��PM=EF��
��DM=8��AN=5��
��EN=8-5=3��
��EM=4��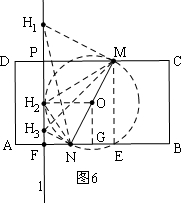
�ɹ��ɶ����ã�MN=5��
��OG��EN��
��NG=$\frac{1}{2}$EN=$\frac{3}{2}$��
��l�ǡ�O�����ߣ�
��OH��l��
ͬ���ã��ı���OGFH�Ǿ��Σ�
��OH=FG=2.5��
��FN=FG-NG=2.5-1.5=1��
�ٵ�0��t��4ʱ����ͼ5����2��H�㣻
�ڵ�t=4ʱ����ͼ6����3��H�㣻
�۵�4��t��5ʱ����ͼ7����4��H�㣻 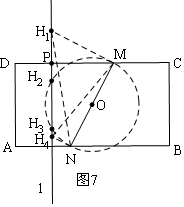
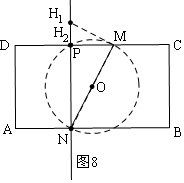
�ܵ�t=5ʱ����ͼ8����2��H�㣻
�ݵ�5��t��8ʱ����ͼ9����4��H�㣻
��t=8ʱ����ͼ10����2��H�㣮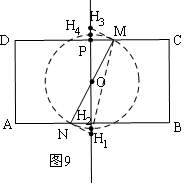
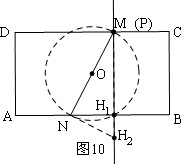
������������0��t��4��t=5��t=8ʱ����2��H�㣻��t=4ʱ����3��H�㣻��4��t��5��5��t��8ʱ����4��H�㣮
���� �������ı��κ�Բ���ۺ��⣬�����˾��ε����ʺ��ж���Բ�ܽǶ������������������ߵ����ʵ�֪ʶ�����Ѷȣ������ǵ�2�ʣ�����Ĺؼ��ǹ�������Բ������ֱ�ߺ�Բ����ʱ��PD�ij�������������ȷ�����������ۣ�Ҫ���ز�©��


 99��1������ĩ��ѵ��ϵ�д�
99��1������ĩ��ѵ��ϵ�д� ��ǿ��У��ĩ���100��ϵ�д�
��ǿ��У��ĩ���100��ϵ�д� �óɼ�1��1��ĩ���100��ϵ�д�
�óɼ�1��1��ĩ���100��ϵ�д� ��״Ԫ���źþ�ϵ�д�
��״Ԫ���źþ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢� | B�� | �٢� | C�� | �٢ۢ� | D�� | �٢ڢۢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
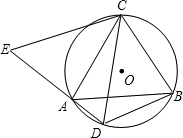 ��ͼ����ABC�ǡ�O���ڽ������Σ�AC=BC��DΪ��O��$\widehat{AB}$��һ�㣬�ӳ�DA����E��ʹCE=CD��
��ͼ����ABC�ǡ�O���ڽ������Σ�AC=BC��DΪ��O��$\widehat{AB}$��һ�㣬�ӳ�DA����E��ʹCE=CD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
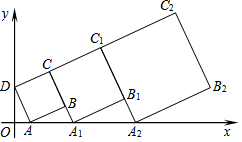 ��ƽ��ֱ������ϵ�У�������ABCD��λ������ͼ��ʾ����A������Ϊ��1��0������D������Ϊ��0��3�����ӳ�CB��x���ڵ�A1����������A1B1C1C���ӳ�C1B1��x���ڵ�A2����������A2B2C2C1���������Ĺ��ɽ�����ȥ����2012�������ε����Ϊ��������
��ƽ��ֱ������ϵ�У�������ABCD��λ������ͼ��ʾ����A������Ϊ��1��0������D������Ϊ��0��3�����ӳ�CB��x���ڵ�A1����������A1B1C1C���ӳ�C1B1��x���ڵ�A2����������A2B2C2C1���������Ĺ��ɽ�����ȥ����2012�������ε����Ϊ��������| A�� | $\sqrt{10}$����$\frac{4}{3}$��4022 | B�� | 10����$\frac{4}{3}$��4022 | C�� | 5����$\frac{4}{3}$��4022 | D�� | 10����$\frac{4}{3}$��4023 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
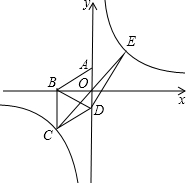 ��ͼ����ƽ��ֱ������ϵ���ı���ABCDΪ���Σ���AD��y���ϣ�����A��0��1����B��-$\sqrt{3}$��0����˫����y=$\frac{m}{x}$������C��
��ͼ����ƽ��ֱ������ϵ���ı���ABCDΪ���Σ���AD��y���ϣ�����A��0��1����B��-$\sqrt{3}$��0����˫����y=$\frac{m}{x}$������C���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com