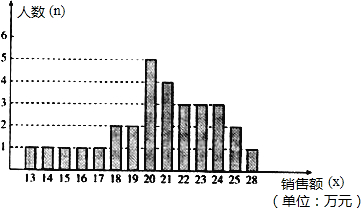
解:(1)由图可知营业员总人数为1+1+1+1+1+2+2+5+4+3+3+3+2+1=30人;
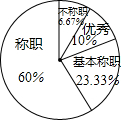
不称职的有2人,所占百分比为

×100%≈6.67%;
基本称职的有7人,所占百分比为
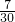
×100%≈23.33%;
称职的有18人,所占百分比为

×100%≈60%;
优秀的有3人,所占百分比为

×100%=10%;
(2)所有称职和优秀的营业员月销售额从小到大排列第11个数为22万元,所以22万元为中位数;
20万元出现了五次,次数最多,为众数.
平均数为:(5×20+4×21+3×22+3×23+3×24+2×25+1×28)÷21≈22万元.
(3)如果要使得称职和优秀这两个层次的所有营业员的半数左右能获奖,这个奖励标准应定为22万元合适
因为称职和优秀的共有21人,月销售额在22万元以上(含22万元)的有12人,超过总数的一半.
分析:(1)首先求出总人数与不称职、基本称职、称职、优秀四个层次营业员人数,进而求出不称职、基本称职、称职、优秀四个层次营业员人数所占百分比,再求出所占的圆心角的度数画图即可解答.
(2)根据中位数、众数和平均数的意义解答即可.
(3)如果要使得称职和优秀这两个层次的所有营业员的半数左右能获奖,月销售额奖励标准可以定为称职和优秀这两个层次销售额的中位数,因为中位数以上的人数占总人数的一半左右.
点评:本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.除此之外,本题也考查了加权平均数、中位数、众数的认识.


 解:(1)由图可知营业员总人数为1+1+1+1+1+2+2+5+4+3+3+3+2+1=30人;
解:(1)由图可知营业员总人数为1+1+1+1+1+2+2+5+4+3+3+3+2+1=30人; ×100%≈6.67%;
×100%≈6.67%;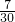 ×100%≈23.33%;
×100%≈23.33%; ×100%≈60%;
×100%≈60%; ×100%=10%;
×100%=10%;