
 24、已知命题:“如图,点A、D、B、E在同一条直线上,且AD=BE,AC∥DF,则△ABC≌△DEF.”这个命题是真命题还是假命题?如果是真命题,请给出证明; 如果是假命题,请添加一个适当的条件,使它成为真命题,并加以证明.
24、已知命题:“如图,点A、D、B、E在同一条直线上,且AD=BE,AC∥DF,则△ABC≌△DEF.”这个命题是真命题还是假命题?如果是真命题,请给出证明; 如果是假命题,请添加一个适当的条件,使它成为真命题,并加以证明.科目:初中数学 来源: 题型:
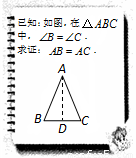
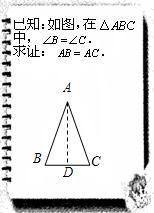 24、文文和彬彬在证明“有两个角相等的三角形是等腰三角形”这一命题时,画出图形,写出“已知”,“求证”(如图),她们对各自所作的辅助线描述如下:
24、文文和彬彬在证明“有两个角相等的三角形是等腰三角形”这一命题时,画出图形,写出“已知”,“求证”(如图),她们对各自所作的辅助线描述如下:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2008年初中毕业升学考试(浙江温州卷)数学(带解析) 题型:解答题
文文和彬彬在证明“有两个角相等的三角形是等腰三角形”这一命题时,画出图形,写出“已知”,“求证”(如图),她们对各自所作的辅助线描述如下:
文文:“过点 作
作 的中垂线
的中垂线 ,垂足为
,垂足为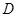 ”;
”;
彬彬:“作 的角平分线
的角平分线 ”.
”.
数学老师看了两位同学的辅助线作法后,说:“彬彬的作法是正确的,而文文的作法需要订正.”
(1)请你简要说明文文的辅助线作法错在哪里.
(2)根据彬彬的辅助线作法,完成证明过程.
查看答案和解析>>
科目:初中数学 来源:2008年初中毕业升学考试(浙江温州卷)数学(解析版) 题型:解答题
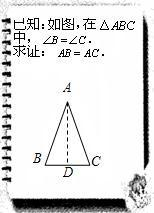
文文和彬彬在证明“有两个角相等的三角形是等腰三角形”这一命题时,画出图形,写出“已知”,“求证”(如图),她们对各自所作的辅助线描述如下:
文文:“过点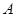 作
作 的中垂线
的中垂线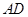 ,垂足为
,垂足为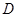 ”;
”;
彬彬:“作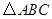 的角平分线
的角平分线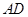 ”.
”.
数学老师看了两位同学的辅助线作法后,说:“彬彬的作法是正确的,而文文的作法需要订正.”
(1)请你简要说明文文的辅助线作法错在哪里.
(2)根据彬彬的辅助线作法,完成证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 要订正.”
要订正.”查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com