
分析 (1)设甲、乙两厂同时处理,每天需x小时,根据共处理垃圾700吨列方程解答即可;
(2)设甲厂每天要处理y吨垃圾,则乙厂每天要处理(700-y)吨垃圾,列出不等式即可解决问题.
解答 解:(1)设甲、乙两厂同时处理,每天需x小时.得:
(55+45)x=700,
解得:x=7,
答:甲、乙两厂同时处理,每天需7小时.
(2)由题知:甲厂处理每吨垃圾费用为
550÷55=10元,
乙厂处理每吨垃圾费用为
495÷45=11元.
设甲厂每天要处理y吨垃圾,则乙厂每天要处理(700-y)吨垃圾,
根据题意得:
则有10y+11(700-y)≤7280,
解得:y≥420.
答:甲厂每天至少要处理420吨垃圾.
点评 本题考查一元一次不等式的应用,将现实生活中的事件与数学思想联系起来,读懂题列出不等式关系式即可求解.注意本题的不等关系为:处理生活垃圾的费用不超过7280元;相等关系为:平均每天产生生活垃圾700吨.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,□ABCO的顶点A、C的坐标分别为A (2,0)、C (-1,2),反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B.
如图,在平面直角坐标系中,□ABCO的顶点A、C的坐标分别为A (2,0)、C (-1,2),反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平移不改变图形的形状,旋转使图形的形状发生改变 | |
| B. | 平移和旋转的共同之处是改变图形的位置和大小 | |
| C. | 一对对应点与旋转中心的距离相等 | |
| D. | 由旋转得到的图形也一定可以通过平移得到 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
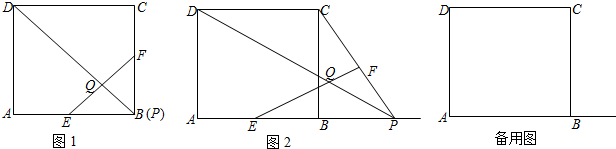
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com