
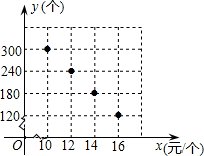
 某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐助给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y (单位:个)与销售单价x(单位:元/个)之间的对应关系如图所示:
某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐助给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y (单位:个)与销售单价x(单位:元/个)之间的对应关系如图所示:分析 (1)直接利用待定系数法求出y与x之间的函数关系式;
(2)利用w=销量×每个利润,进而得出函数关系式;
(3)利用进货成本不超过900元,得出x的取值范围,进而得出函数最值.
解答 解:(1)设y=kx+b,
根据题意可得:$\left\{\begin{array}{l}{10k+b=300}\\{12k+b=240}\end{array}\right.$,
解得;$\left\{\begin{array}{l}{k=-30}\\{b=600}\end{array}\right.$,
故y与x之间的函数关系是:y=-30x+600;
故答案为:y=-30x+600;
(2)由题意得:
w=(x-6)(-30x+600)
=-30x2+780x-3600,
∴w与x的函数关系式为w=-30x2+780x-3600;
(3)由题意得:6(-30x+600)≤900,
解得:x≥15,
在w=-30x2+780x-3600中,对称轴为:x=-$\frac{780}{2×(-30)}$=13,
∵a=-30,∴当x>13时,w随x的增大而减小,
∴x=15时,w最大为:(15-6)(-30×15+600)=1350,
∴销售单价定为每个15元时,利润最大为1350元.
点评 此题主要考查了待定系数法求一次函数解析式以及二次函数的应用,正确得出w与x之间的函数关系式是解题关键.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
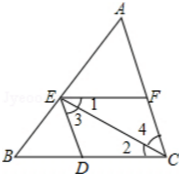
| A. | ∠1=∠3 | B. | ∠3=∠A | C. | ∠1=∠2 | D. | ∠1=∠A |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
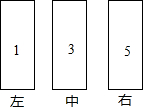 如图,敲击三根管时依次发出“1”、“3”“5”,两只音锤同时从“1”开始,以相同的节拍往复敲击,不同的是:甲锤每拍移动一位(左中右中左中右…),乙锤则在两端各有一拍不移位(左中右右中左左中右…),在第200拍时,你听到的是( )
如图,敲击三根管时依次发出“1”、“3”“5”,两只音锤同时从“1”开始,以相同的节拍往复敲击,不同的是:甲锤每拍移动一位(左中右中左中右…),乙锤则在两端各有一拍不移位(左中右右中左左中右…),在第200拍时,你听到的是( )| A. | 同样的音“1” | B. | 同样的音“3” | C. | 同样的音“5” | D. | 不同的两个音 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD为⊙O的内接四边形,对边BC,AD交于点F,AB、DC交于点E,△ECF的外接圆与⊙O的另一交点为H,AH与EF交于点M,MC与⊙O交于点C.证明:
如图,四边形ABCD为⊙O的内接四边形,对边BC,AD交于点F,AB、DC交于点E,△ECF的外接圆与⊙O的另一交点为H,AH与EF交于点M,MC与⊙O交于点C.证明:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com