
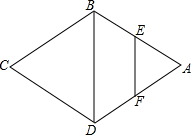
 如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点,若EF=2,求菱形的周长.
如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点,若EF=2,求菱形的周长.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
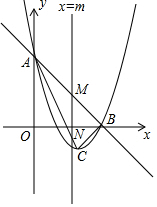 如图,已知抛物线y=x2+bx+c与直线y=-x+3相交于坐标轴上的A,B两点,顶点为C.
如图,已知抛物线y=x2+bx+c与直线y=-x+3相交于坐标轴上的A,B两点,顶点为C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
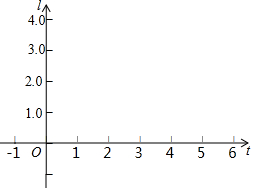 某学生发现学校的电动伸缩门从宪全收拢到完全打开的过程中,电动伸缩门伸缩后的总长度1(米)与按电钮开关的时间t(秒)之间存在某种函数关系(电动伸缩门初始状态是完全收拢的).经几次试验后,得到一组对应数据如下:
某学生发现学校的电动伸缩门从宪全收拢到完全打开的过程中,电动伸缩门伸缩后的总长度1(米)与按电钮开关的时间t(秒)之间存在某种函数关系(电动伸缩门初始状态是完全收拢的).经几次试验后,得到一组对应数据如下:| t(秒) | 0 | 1 | 2 | 3 | 4 | 5 | … |
| l(米) | 1 | 1.4 | 1.8 | 2.2 | 2.6 | 3.0 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,抛物线y=-x2+2mx-3+4m-m2的对称轴是直线x=1
在平面直角坐标系xOy中,抛物线y=-x2+2mx-3+4m-m2的对称轴是直线x=1查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在Rt△ABC中,∠C=90°,∠A=30°,AB=6,点D,E分别是BC,AB上的动点,将△BDE沿直线DE翻折,点B的对应点B′恰好落在AC上,若△AEB′是等腰三角形,那么CB′的值是3,3$\sqrt{2}$-3,0.
在Rt△ABC中,∠C=90°,∠A=30°,AB=6,点D,E分别是BC,AB上的动点,将△BDE沿直线DE翻折,点B的对应点B′恰好落在AC上,若△AEB′是等腰三角形,那么CB′的值是3,3$\sqrt{2}$-3,0.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
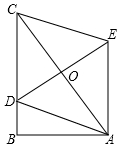 如图,在Rt△ABC中,∠B=90°,∠BAC=60°,AB=1,点D在BC边上,以AC为对角线的平行四边形ADCE中,当DE的长最小时,平行四边形ADCE的面积为$\frac{\sqrt{3}}{2}$.
如图,在Rt△ABC中,∠B=90°,∠BAC=60°,AB=1,点D在BC边上,以AC为对角线的平行四边形ADCE中,当DE的长最小时,平行四边形ADCE的面积为$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com