
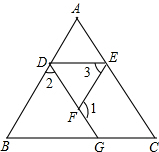
 如图,已知∠1+∠2=180°,∠B=∠3,判断∠C与∠AED的大小关系,并说明理由.
如图,已知∠1+∠2=180°,∠B=∠3,判断∠C与∠AED的大小关系,并说明理由. 科目:初中数学 来源: 题型:选择题
 如图,如果CD是Rt△ABC的中线,∠ACB=90°,∠A=50°,那么∠CDB等于( )
如图,如果CD是Rt△ABC的中线,∠ACB=90°,∠A=50°,那么∠CDB等于( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在梯形ABCD中,AD∥BC,∠C=36°,∠B=54°,点M、N分别是AD、BC的中点,如果BC=10,AD=4,那么MN的长是3.
如图,在梯形ABCD中,AD∥BC,∠C=36°,∠B=54°,点M、N分别是AD、BC的中点,如果BC=10,AD=4,那么MN的长是3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某市自来水公司为了鼓励市民节约用水采取了分段收费标准,某户居民每月应交水费y(元)与水量x(吨)之间的关系图象如图所示:
某市自来水公司为了鼓励市民节约用水采取了分段收费标准,某户居民每月应交水费y(元)与水量x(吨)之间的关系图象如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com