
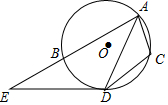
 如图,已知AD是⊙O的弦,$\widehat{BD}$=$\widehat{CD}$,DE是⊙O的切线且与弦AB的延长线相交于点E,若AC=3,AE=8,则AD的长为2$\sqrt{6}$.
如图,已知AD是⊙O的弦,$\widehat{BD}$=$\widehat{CD}$,DE是⊙O的切线且与弦AB的延长线相交于点E,若AC=3,AE=8,则AD的长为2$\sqrt{6}$. 分析 如图,连接BD、BC,构建相似三角形△AED∽△ADC,由该相似三角形的对应边成比例来求AD的长度.
解答  解:如图,连接BD、BC.
解:如图,连接BD、BC.
∵$\widehat{BD}$=$\widehat{CD}$,
∴∠BAD=∠CAD,即∠DAE=∠CAD
∵DE为圆O切线,
∴∠EDB=∠BCD,∠BDA=∠BCA,
∴∠EDB+∠BDA=∠BCD+∠BCA,即∠EDA=∠DCA,
∴△AED∽△ADC,
∴AE:AD=AD:AC,
∴AD2=AC•AE,
∵AC=3,AE=8,
∴AD2=24,
∴AD=2$\sqrt{6}$.
故答案是:2$\sqrt{6}$.
点评 本题考查了切线的性质,圆周角、弧、弦的关系,三者关系可理解为:在同圆或等圆中,①圆心角相等,②所对的弧相等,③所对的弦相等,三项“知一推二”,一项相等,其余二项皆相等.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
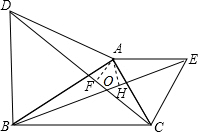 如图,已知△ABD,△AEC都是等边三角形,AF⊥CD于F,AH⊥BE于H,问:
如图,已知△ABD,△AEC都是等边三角形,AF⊥CD于F,AH⊥BE于H,问:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com