
分析 根据抛物线与x轴有两个不同的交点,根的判别式△>0,再分a>0和a<0两种情况对各选项讨论即可得解.
解答 解:
∵二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点无法确定a的正负情况,
∴选项②项错误;
∵二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点,且坐标分别为(x1,0)、(x2,0),且x1<x2,
∴b2-4ac>0,故选项③错误;
若a>0,则x1<x0<x2,
若a<0,则x0<x1<x2或x1<x2<x0,故选项④错误
若a>0,则x0-x1>0,x0-x2<0,
∴(x0-x1)(x0-x2)<0,
∴a(x0-x1)(x0-x2)<0,
若a<0,则(x0-x1)与(x0-x2)同号,
∴a(x0-x1)(x0-x2)<0,
综上所述,a(x0-x1)(x0-x2)<0正确,故选项①正确,
故答案为:①.
点评 本题考查了二次函数与x轴的交点问题,熟练掌握二次函数图象以及图象上点的坐标特征是解题的关键,①选项要注意分情况讨论.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
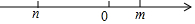 对于有理数m,n,定义一种新运算,规定m?n=|m+n|-|m-n|
对于有理数m,n,定义一种新运算,规定m?n=|m+n|-|m-n|查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
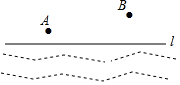 如图,L为汀江河的南岸线,一天傍晚某牧童在A处放牛,欲将牛牵到河边饮水后再回到家B处,牧童想以最短的路程回家.请你在图中画出牛饮水C的位置.(保留痕迹)
如图,L为汀江河的南岸线,一天傍晚某牧童在A处放牛,欲将牛牵到河边饮水后再回到家B处,牧童想以最短的路程回家.请你在图中画出牛饮水C的位置.(保留痕迹)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com