练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    对于实数a，b，我们定义符号max{a，b}的意义为：当a≥b时，max{a，b}=a；当a＜b时，max{a，b]=b；如：max{4，﹣2}=4，max{3，3}=3，若关于x的函数为y=max{x+3，﹣x+1}，则该函数的最小值是（　　）

    A. 0 B. 2 C. 3 D. 4

    B 【解析】试题分析：当x+3≥﹣x+1，即：x≥﹣1时，y=x+3，∴当x=﹣1时，ymin=2， 当x+3＜﹣x+1，即：x＜﹣1时，y=﹣x+1，∵x＜﹣1，∴﹣x＞1，∴﹣x+1＞2，∴y＞2，∴ymin=2，
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：广西合浦县2017年秋季学期教学质量监测七年级数学试卷 题型：单选题

    如图，正比例函数y=x与反比例函数y= 的图象相交于A、B两点，分别过A、B两点作y轴的垂线，垂足分别为C、D，连接AD，BC，则四边形ACBD的面积为（ ）

    A. 2 B. 4 C. 6 D. 8

    B 【解析】将正比例函数y=?x代入到反比例函数y=?2x中得： ?x=?2x,整理得： ， 解得：x=±2 ， ∴点A的坐标为(?,)、点B的坐标为(,?)， ∴AC=BD= ,OC=OD= . 故选B。

    查看答案和解析>>

    科目：初中数学 来源：山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型：填空题

    已知点都在二次函数的图象上，则y1, y2 , y3的大小关系是______ 。

    【解析】试题分析：把A（4，y1），B（，y2），C（－2，y3）分别代入y＝(x－2)2－1得： y1＝(4－2)2－1＝3，y2＝(－2)2－1＝5－，y3＝(－2－2)2－1＝15， ∵5－＜3＜15， 所以y3＞y1＞y2． 故答案为：y3＞y1＞y2．

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十九章达标检测卷 题型：解答题

    如图所示，在平面直角坐标系中，已知一次函数y=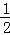x+1的图象与x轴，y轴分别交于A，B两点，以AB为边在第二象限内作正方形ABCD．

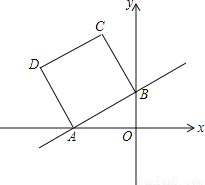
    （1）求边AB的长；

    （2）求点C，D的坐标；

    （3）在x轴上是否存在点M，使△MDB的周长最小？若存在，请求出点M的坐标；若不存在，请说明理由．

    （1）；（2）C（﹣1，3），D（﹣3，2）；（3）M（﹣1，0）． 【解析】 试题分析：（1）在直角三角形AOB中，由OA与OB的长，利用勾股定理求出AB的长即可； （2）过C作y轴垂线，过D作x轴垂线，分别交于点E，F，可得三角形CBE与三角形ADF与三角形AOB全等，利用全等三角形对应边相等，确定出C与D坐标即可； （3）作出B关于x轴的对称点B′，连接B′D，与x轴...

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十九章达标检测卷 题型：填空题

    直线y=3x+6与两坐标轴围成的三角形的面积是______.

    6 【解析】试题解析：∵直线y=3x+6与两坐标轴的交为（0，6），（-2，0）， ∴直线y=3x+6与两坐标轴围成的三角形的面积=×6×2=6．

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十九章达标检测卷 题型：单选题

    关于x的一次函数y=kx+k2+1的图象可能正确的是（　　）

    A. B. C. D.

    C 【解析】试题分析：根据图象与y轴的交点直接解答即可． 【解析】 令x=0，则函数y=kx+k2+1的图象与y轴交于点（0，k2+1），∵k2+1＞0，∴图象与y轴的交点在y轴的正半轴上． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：2018人教版九年级数学下册练习：第二十八章 达标检测卷 题型：解答题

    为倡导“低碳生活”，人们常选择以自行车作为代步工具，如图是一辆自行车的部分几何示意图，其中车架档AC与CD的长分别为45 cm和60 cm，且它们互相垂直，座杆CE的长为20 cm，点A，C，E在同一条直线上，且∠CAB＝75°.(参考数据：sin 75°≈0.966，cos 75°≈0.259，tan 75°≈3.732)

    （1）求车架档AD的长；

    （2）求车座点E到车架档AB的距离(结果精确到1 cm)．

    （1）车架档AD的长是75 cm；（2）车座点E到车架档AB的距离约为63 cm. 【解析】试题分析：（1）在Rt△ACD中利用勾股定理求AD即可。 （2）过点E作EF⊥AB，在Rt△EFA中，利用三角函数求EF=AEsin75°，即可得到答案。 试题解析：(1)在Rt△ACD中，AC＝45 cm，DC＝60 cm， ∴AD＝＝75(cm)， ∴车架档AD的长是75 ...

    查看答案和解析>>

    科目：初中数学 来源：2018人教版九年级数学下册练习：第二十八章 达标检测卷 题型：单选题

    在Rt△ABC中，∠C＝90°，∠A，∠B，∠C的对边分别为a，b，c，则下列式子一定成立的是(　　)

    A. a＝c·sin B B. a＝c·cos B C. b＝c·sin A D. b＝

    B 【解析】试题分析：本题可以利用锐角三角函数的定义代入求解即可．在Rt△ABC中，∠C=90°，则cosA=，sinA=，tanB=，cosB=，tanA=，cotA=，因而b=c•cosA=a•tanB，a=c•sinA=c•cosB=b•tanA=，所以，一定成立的是a=c•cosB． 故选：B．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学北师大版上册 第1章 丰富的图形世界 单元测试卷 题型：单选题

    将四个棱长为1的正方体如图摆放，则这个几何体的表面积是（　　）

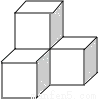
    A. 3 B. 9 C. 12 D. 18

    D 【解析】试题分析：观察几何体，得到这个几何体向前、向后、向上、向下、向左、向右分别有3个正方形，则它的表面积=6×3×1=18． 故选：D．

    查看答案和解析>>

    同步练习册答案