
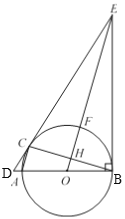
【题目】如图,AB是⊙O的直径,C 是⊙O上一点,过点C 作⊙O的切线,交BA的延长线交于点D,过点B 作BE⊥BA,交DC延长线于点E,连接OE,交⊙O于点F,交BC于点H,连接AC.
(1)求证:∠ECB=∠EBC;
(2)连接BF,CF,若BF=5,sin∠FBC=![]() ,求AC的长.
,求AC的长.
【答案】(1)见详解;(2)![]()
【解析】
(1)先证EB为⊙O的切线,再利用切线长定理即可证得∠ECB=∠EBC;
(2)先由BF=5,sin∠FBC=![]() 求得FH及HB的长,再由Rt△BOH的勾股定理求得OH长,最后利用中位线即可求得AC的长.
求得FH及HB的长,再由Rt△BOH的勾股定理求得OH长,最后利用中位线即可求得AC的长.
(1)证明:∵BE⊥BA,AB是⊙O的直径,
∴BE是⊙O的切线,
又∵CE是⊙O的切线,
∴BE=CE,
∴∠ECB=∠EBC;
(2)解:如图,连接OC,
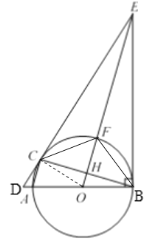
∵BE=CE,OB=OC,
∴OE垂直平分BC,
∴∠BHF=∠BHO=90°,点H为BC的中点,
∴在Rt△BHF中,sin∠FBC=![]() =
=![]() ,
,
∵BF=5,
∴FH=3,
∴BH=![]() ,
,
设OH=x,则OB=OF=x+3,
在Rt△OHB中,OH2+BH2=OB2,
∴x2+42=(x+3)2,
解得x=![]()
∴OH=![]()
∵点O、H分别为AB、CB的中点,
∴OH是△ABC的中位线,
∴AC=2OH=![]()


科目:初中数学 来源: 题型:
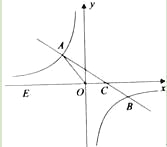
【题目】如图,在平面直角坐标系x0y中,一次函数y=kx+b(k≠0)的图象与反比例函数![]() (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且sin∠AOE=
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且sin∠AOE=![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)求△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“长跑”是中考体育考试项目之一.某中学为了解九年级学生“长跑”的情况,随机抽取部分九年级学生,测试其长跑成绩(男子1000米,女子800米),按长跑的时间的长短依次分为A,B,C,D四个等级进行统计,并绘制成如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
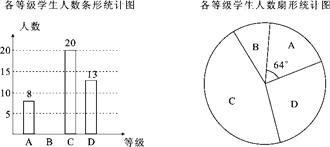
(1)在这次调查中共抽取了 名学生,扇形统计图中,D类所对应的扇形圆心角大小为 ;
(2)所抽取学生“长跑”测试成绩的中位数会落在 等级;
(3)若该校九年级共有900名学生,请你估计该校C等级的学生约在多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中雅培粹学校举办运动会,全校有3000名同学报名参加校运会,为了解各类运动赛事的分布情况,从中抽取了部分同学进行统计:A.田径类,B.球类,C.团体类,D.其他,并将统计结果绘制成如图所示的两幅不完整的统计图.

(1)这次统计共抽取了 位同学,扇形统计图中的![]() ,
,![]() 的度数是 ;
的度数是 ;
(2)请将条形统计图补充完整;
(3)估计全校共多少学生参加了球类运动.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠PAQ=36°,点B为射线AQ上一固定点,按以下步骤作图:①分别以A,B为圆心,大于![]() AB的长为半径画弧,相交于两点M,N;②作直线MN交射线AP 于点D,连接 BD;③以B为圆心,BA长为半径画弧,交射线AP 于点C; 根据以上作图过程及所作图形,下列结论中错误的是( )
AB的长为半径画弧,相交于两点M,N;②作直线MN交射线AP 于点D,连接 BD;③以B为圆心,BA长为半径画弧,交射线AP 于点C; 根据以上作图过程及所作图形,下列结论中错误的是( )
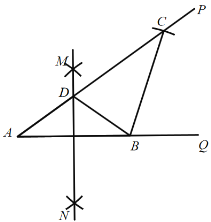
A.∠CDB=72°B.△ADB∽△ABCC.CD:AD=2:1D.∠ABC=3∠ACB
查看答案和解析>>
科目:初中数学 来源: 题型:
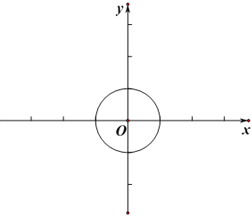
【题目】对于平面直角坐标系xOy中的点P和⊙C,给出如下的定义:若⊙C上存在两个点A、B,使得∠APB=60°,则称P为⊙C的可视点.
(1)当⊙O的半径为1时,
①在点![]() 、E(1,1)、F(3,0)中,⊙O的可视点是______.
、E(1,1)、F(3,0)中,⊙O的可视点是______.
②过点M(4,0)作直线l:y=kx+b,若直线l上存在⊙O的可视点,求b的取值范围;
(2)若T(t,0),⊙T的半径为1,直线y=![]() 上存在⊙T的可视点,且所有可视点构成的线段长度为n,若
上存在⊙T的可视点,且所有可视点构成的线段长度为n,若![]() ,直接写出t 的取值范围.
,直接写出t 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式更多样、便捷某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
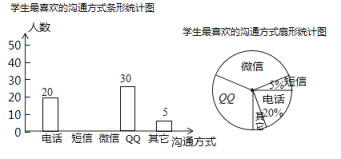
(1)这次统计共抽查了多少名学生?在扇形统计图中,表示" ![]() "的扇形圆心角的度数是多少;
"的扇形圆心角的度数是多少;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用 “微信”进行沟通的学生大约有多少名?
(4)某天甲、乙两名同学都想从“微信"、"![]() "、“电话"三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.
"、“电话"三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
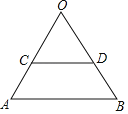
【题目】如图,△ABO是正三角形,CD∥AB,把△ABO绕△OCD的内心P旋转180°得到△EFG
(1)在图中画出点P和△EFG,保留画图痕迹,简要说明理由
(2)若AO=3![]() ,CD=2
,CD=2![]() ,求A点运动到E点路径的长.
,求A点运动到E点路径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
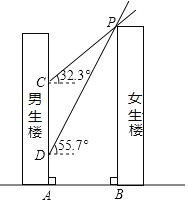
【题目】如图,男生楼在女生楼的左侧,两楼高度均为90m,楼间距为AB,冬至日正午,太阳光线与水平面所成的角为![]() ,女生楼在男生楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为
,女生楼在男生楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为![]() ,女生楼在男生楼墙面上的影高为DA,已知
,女生楼在男生楼墙面上的影高为DA,已知![]() .
.
![]() 求楼间距AB;
求楼间距AB;
![]() 若男生楼共30层,层高均为3m,请通过计算说明多少层以下会受到挡光的影响?
若男生楼共30层,层高均为3m,请通过计算说明多少层以下会受到挡光的影响?![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com