
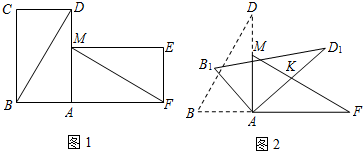
���� ��1����������ȫ�غϵľ���ֽƬ��С��ͬѧ������һ���Ƶ�A˳ʱ����ת90���õ�����AMEF����ͼ1������BD=MF����BAD�ա�MAF���Ƴ�BD=MF����ADB=��AFM=30�㣬�����ɵá�DNM�Ĵ�С��
��2��������ת�����ʵó����ۣ�
��3�����жϳ��ص��������������Ǹտ�ʼ��ת��BD�պù���M�����ɸ�����ת�������жϳ���AB1M�ǵȱ������μ��ɵó����ۣ������ݺ�30���ֱ�������ε����ʼ������AM��MK�������ζ������ʽ���ɵó����ۣ�
��� �⣺��1��BD��MF��
�ӳ�FM��BD�ڵ�N��
������ã���BAD�ա�MAF��
��BD=MF����ADB=��AFM=30�㣮
�֡ߡ�DMN=��AMF��
���ADB+��DMN=��AFM+��AMF=90�㣬
���DNM=90�㣬
��BD��MF��
�ʴ�Ϊ��BD��MF��
��2����AK=FKʱ����KAF=��AFM=30�㣬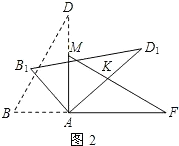
���BAB1=180��-��B1AD1-��KAF=180��-90��-30��=60�㣬
����=60�㣻
�ڵ�AF=FKʱ����FAK=$\frac{180��-��AFM}{2}$=75�㣬
���BAB1=90��-��FAK=15�㣬
����=15�㣻
��µĶ���Ϊ60���15��
��3����ͼ3��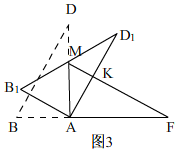
��ABD����ת�Ĺ����У��տ�ʼ��ת����AB1D1�͡�AMF���ص�����Ϊ�����Σ���ʱ��ת�Ǧ£�0��
BD����ת���պù���Mʱ���ص�����Ҳ�������Σ���ʱ��AM=AB��
��Rt��ABD�У���ADB=30�㣬
���ABD=60�㣬
����ת֪����AB1D1=��ABD=60�㣬
���AB1MΪ�ȱ������Σ�
���B1AM=60�㣬
���BAB1=30�㣬����=30�㣬
��0�㣼�¡�30�㣬
����=30��ʱ����AB1D1�͡�AMF�غϲ����������Σ���ͼ3����AMK��
�ߡ�B1AM=60�㣬
���MAK=30�㣬
�ߡ�AMF=60�㣬
���AKM=90�㣬
��Rt��AMF�У���AFM=30�㣬AF=2��
��AM=$\frac{2\sqrt{3}}{3}$��
��Rt��AMK�У���MAK=30�㣬AM=$\frac{2\sqrt{3}}{3}$��
��MK=$\frac{1}{2}$AM=$\frac{\sqrt{3}}{3}$��AK=$\sqrt{3}$MK=1��
��S��AMK=$\frac{1}{2}$MK��AK=$\frac{1}{2}$��$\frac{\sqrt{3}}{3}$��1=$\frac{\sqrt{3}}{6}$��
��������=30��ʱ����AB1D1�͡�AMF�غϲ��ֵ����Ϊ$\frac{\sqrt{3}}{6}$cm2��
���� �������ı����ۺ��⣬��Ҫ�����˾��ε����ʣ�ֱ�������ε����ʣ��ȱ������ε��ж������ʣ������ε������ʽ����ת�����ʣ��Ȿ��Ĺؼ���������ת�����ʵ�ͬʱҪ������ã�


 ����˼ά�żӿ���ϵ�д�
����˼ά�żӿ���ϵ�д� �����Ծ�ϵ�д�
�����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2016-2017ѧ���㽭ʡ���꼶3���¿���ѧ�Ծ��������棩 ���ͣ������
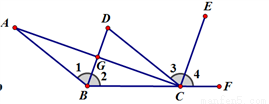
��ͼ��CD//AB��BDƽ�֡�ABC��CEƽ�֡�DCF����ACE=90��
��1������BD��CE�Ƿ�ƽ�У�����˵�����ɣ�
��2��AC��BD�к�λ�ù�ϵ������˵���жϵ����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
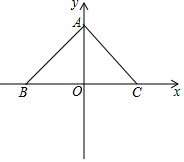 ��ͼ����ƽ��ֱ������ϵ�У���A��B��C�����������ϣ�AO=BO=CO��BC=8��
��ͼ����ƽ��ֱ������ϵ�У���A��B��C�����������ϣ�AO=BO=CO��BC=8���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
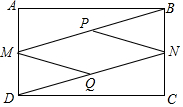 ��֪����ͼ���ھ���ABCD�У�M��N�ֱ���AB��DC���е㣬P��Q�ֱ���DM��BN���е㣮
��֪����ͼ���ھ���ABCD�У�M��N�ֱ���AB��DC���е㣬P��Q�ֱ���DM��BN���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
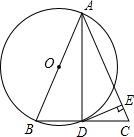 ��ͼ��ʾ���ڡ�ABC�У�AB=AC����ABΪֱ������O����BC��D��DE��AC��E��
��ͼ��ʾ���ڡ�ABC�У�AB=AC����ABΪֱ������O����BC��D��DE��AC��E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com