
【题目】以四边形ABCD的边AB,AD为边分别向外侧作等边△ABF和等边△ADE,连接EB,FD,交点为G.
(1)当四边形ABCD为正方形时(如图1),EB和FD的数量关系是 ;
(2)当四边形ABCD为矩形时(如图2),EB和FD具有怎样的数量关系?请加以证明;
(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD是否发生变化?如果改变,请说明理由.
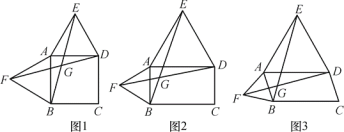
【答案】(1)EB=FD;(2)EB=FD,证明见解析;(3)∠EGD不发生变化.
【解析】
(1)利用正方形的性质、等边三角形的性质和全等三角形的证明方法可证明△FAD≌△BAE,由全等三角形的性质即可得到EB= FD;
(2)利用长方形的性质、等边三角形的性质和全等三角形的证明方法可证明△FAD≌△BAE,由全等三角形的性质即可得到EB= FD;
(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD不会发生变化,是一个定值,为60°.
解:(1)EB=FD,
理由如下:

∵四边形ABCD为正方形,
∴AB=AD,
∵以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE,
∴AF=AE,∠FAB=∠EAD=60°,
∵∠FAD=∠BAD+∠FAB=90°+60°=150°,
∠BAE=∠BAD+∠EAD=90°+60°=150°,
∴∠FAD=∠BAE,
在△AFD和△ABE中,
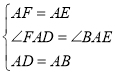 ,
,
∴△AFD≌△ABE,
∴EB=FD;
(2)EB=FD.
证:∵△AFB为等边三角形
∴AF=AB,∠FAB=60°
∵△ADE为等边三角形,
∴AD=AE,∠EAD=60°
∴∠FAB+∠BAD=∠EAD+∠BAD,
即∠FAD=∠BAE
∴△FAD≌△BAE
∴EB=FD;
(3)解:不会发生改变;

同(2)易证:△FAD≌△BAE,
∴∠AEB=∠ADF,
设∠AEB为x°,则∠ADF也为x°
于是有∠BED为(60﹣x)°,∠EDF为(60+x)°,
∴∠EGD=180°﹣∠BED﹣∠EDF
=180°﹣(60﹣x)°﹣(60+x)°
=60°.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以OA1对角线为边作正方形OA1A2B1,再以正方形的对角线OA2作正方形OA1A2B1,…,依此规律,则点A2017的坐标是( )
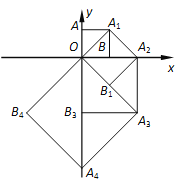
A. (0,21008) B. (21008,21008) C. (21009,0) D. (21009,-21009)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
通过整式运算一章的学习,我们发现要验证一个结论的正确性可以有两种方法:
例如:要验证结论![]()
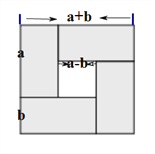
方法1:几何图形验证:如下图,我们可以将一个边长为(a+b)的正方形上裁去一个边长为(a-b)的小正方形则剩余图形的面积为4ab,验证该结论正确。
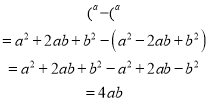
方法2:代数法验证:等式左边=![]() ,
,
所以,左边=右边,结论成立。
观察下列各式:
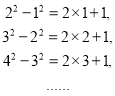
(1)按规律,请写出第n个等式________________;
(2)试分别用两种方法验证这个结论的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
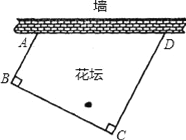
【题目】小区要用篱笆围成一个四边形花坛、花坛的一边利用足够长的墙,另三边所用的篱笆之和恰好为18米.围成的花坛是如图所示的四边形ABCD,其中∠ABC=∠BCD=90°,且BC=2AB.设AB边的长为x米.四边形ABCD面积为S平方米.
(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围).
(2)当x是多少时,四边形ABCD面积S最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-2![]() x+m=0有两个不相等的实数根.
x+m=0有两个不相等的实数根.
(1)求实数m的最大整数值;
(2)在(1)的条件下,方程的实数根是x1,x2,求代数式![]() +
+![]() -
-![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
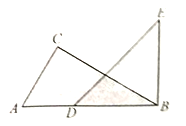
【题目】如图,一副三角板的三个内角分别是![]() ,
,![]() ,
,![]() 和
和![]() ,
,![]() ,
,![]() ,按如图所示叠放在一起(点
,按如图所示叠放在一起(点![]() 在同一直线上),若固定
在同一直线上),若固定![]() ,将
,将![]() 绕着公共顶点
绕着公共顶点![]() 顺时针旋转
顺时针旋转![]() 度(
度(![]() ),当边
),当边![]() 与
与![]() 的某一边平行时,相应的旋转角
的某一边平行时,相应的旋转角![]() 的值为_______.
的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
对于多项式![]() ,如果我们把
,如果我们把![]() 代入此多项式,发现
代入此多项式,发现![]() 的值为0,这时可以确定多项式中有因式
的值为0,这时可以确定多项式中有因式![]() :同理,可以确定多项式中有另一个因式
:同理,可以确定多项式中有另一个因式![]() ,于是我们可以得到:
,于是我们可以得到:![]() .
.
又如:对于多项式![]() ,发现当
,发现当![]() 时,
时,![]() 的值为0,则多项式
的值为0,则多项式![]() 有一个因式
有一个因式![]() ,我们可以设
,我们可以设![]() ,解得
,解得![]() ,
,![]() ,于是我们可以得到:
,于是我们可以得到:![]() .
.
请你根据以上材料,解答以下问题:
(1)当![]() 时,多项式
时,多项式![]() 的值为0,所以多项式
的值为0,所以多项式![]() 有因式 ,从而因式分解
有因式 ,从而因式分解![]() .
.
(2)以上这种因式分解的方法叫试根法,常用来分解一些比较复杂的多项式.请你尝试用试根法分解多项式:①![]() ;②
;②![]() .
.
(3)小聪用试根法成功解决了以上多项式的因式分解,于是他猜想:
代数式![]() 有因式 , , ,
有因式 , , ,
所以分解因式![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着O﹣A﹣B﹣C﹣O的路线移动(即沿长方形移动一周).
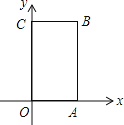
(1)写出B点的坐标;
(2)当点P移动3秒时,求三角形OAP的面积;
(3)在移动过程中,当点P到x轴距离为4个单位长度时,求点P移动的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的中线BD,CE交于点O,F,G分别是BO,CO的中点.
(1)求证:四边形DEFG是平行四边形.
(2)若AB=AC,则四边形DEFG是 (填写特殊的平行四边形).
(3)若四边形DEFG是边长为2的正方形,试求△ABC的周长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com