
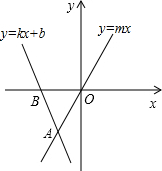
 如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为x<-1.
如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为x<-1.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两墙足够长)用26m长的篱笆围成一个矩形花园ABCD(篱笆只围AB、BC两边),设AB=x m.
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两墙足够长)用26m长的篱笆围成一个矩形花园ABCD(篱笆只围AB、BC两边),设AB=x m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
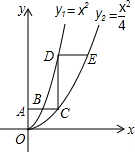 如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与y2=$\frac{{x}^{2}}{4}$(x≥0)于B,C两点,过点C作y轴的平行交y1于点D,直线DE∥AC,交y2于点E,则$\frac{DE}{AB}$=2.
如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与y2=$\frac{{x}^{2}}{4}$(x≥0)于B,C两点,过点C作y轴的平行交y1于点D,直线DE∥AC,交y2于点E,则$\frac{DE}{AB}$=2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
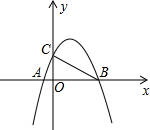 二次函数y=一x2+ax+b图象与x轴交于A($-\frac{1}{2}$,0),B(2,0)两点,且与y轴交于点C.
二次函数y=一x2+ax+b图象与x轴交于A($-\frac{1}{2}$,0),B(2,0)两点,且与y轴交于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com