

分析 (1)利用配方法或公式法求顶点坐标,求出最小AE即可求出点F坐标.
(2)如图1中,作点F关于对称轴的对称点F′,连接FF′交对称轴于G,在CF上取一点C′,使得CC′=$\sqrt{2}$,连接C′F′与对称轴交于点N,此时四边形CMNF周长最小.
(3)分两种情形①PG∥FB时;②如图3中,PG′=PG=2$\sqrt{2}$,作PM⊥BD于M,QK⊥PD于K,QJ⊥PD′于J.分别求解即可.
解答 解:(1)∵y=$\frac{\sqrt{2}}{4}$x2-2x-6$\sqrt{2}$=$\frac{\sqrt{2}}{4}$(x-2$\sqrt{2}$)2-8$\sqrt{2}$,
∴顶点D坐标(2$\sqrt{2}$,-8$\sqrt{2}$),
由题意E(4$\sqrt{2}$,-8$\sqrt{2}$),A(-2$\sqrt{2}$,0),B(6$\sqrt{2}$,0),
设直线AE解析式为y=kx+b,则有$\left\{\begin{array}{l}{-2\sqrt{2}k+b=0}\\{4\sqrt{2}k+b=-8\sqrt{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-1}\\{b=-2\sqrt{2}}\end{array}\right.$,
∴直线AE解析式为y=-x-2$\sqrt{2}$,
∴点F坐标(0,-2$\sqrt{2}$).
(2)如图1中,作点F关于对称轴的对称点F′,连接FF′交对称轴于G,在CF上取一点C′,使得CC′=$\sqrt{2}$,连接C′F′与对称轴交于点N,此时四边形CMNF周长最小.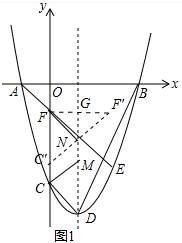
∵四边形CMNF的周长=CF+NM+CM+FN=5$\sqrt{2}$+CM+NF,CM+NF=C′N+NF=C′N+NF′=C′F′(两点之间线段最短),
∴此时四边形CMNF的周长最小.
∵C′F=3$\sqrt{2}$
∴GN=$\frac{1}{2}$C′F=$\frac{3\sqrt{2}}{2}$,
∴-(a+$\sqrt{2}$)=2$\sqrt{2}$+$\frac{3}{2}$$\sqrt{2}$,
∴a=-$\frac{9\sqrt{2}}{2}$,
∵C′F′=$\sqrt{(4\sqrt{2})^{2}+(3\sqrt{2})^{2}}$=5$\sqrt{2}$,
∴四边形CMNF的周长最小值=5$\sqrt{2}$+5$\sqrt{2}$=10$\sqrt{2}$.
(3)如图2中,作PF⊥BD于F,QH⊥对称轴于H.
由题意可知BD=$\sqrt{(4\sqrt{2})^{2}+(8\sqrt{2})^{2}}$=4$\sqrt{10}$,DQ=2$\sqrt{10}$t,
∵S△PQG=$\frac{1}{2}$S△DPQ=$\frac{1}{2}$S△PD′Q,
∴PG=$\frac{1}{2}$PD′=$\frac{1}{2}$PD=2$\sqrt{2}$=$\frac{1}{2}$BF,
情形①PG∥FB时,∵PF=PD,
∴BG=GD,
∴PG=$\frac{1}{2}$BF=2$\sqrt{2}$,
在Rt△QHD中,sin∠HDQ=$\sqrt{5}$,DQ=2$\sqrt{10}$t,
∴HQ=2$\sqrt{2}$t,HD=4$\sqrt{2}$t,
∵∠QPD′=∠QPD=45°,
∴PH=HQ=2$\sqrt{2}$t,
∴PH+HD=PD,
∴6$\sqrt{2}$t=4$\sqrt{2}$,
∴t=$\frac{2}{3}$.
情形②如图3中,PG′=PG=2$\sqrt{2}$,作PM⊥BD于M,QK⊥PD于K,QJ⊥PD′于J.
由sin∠PDG=sin∠GPM=$\frac{1}{\sqrt{5}}$=$\frac{MG}{PG}$,
∴MG′=MG=$\frac{2\sqrt{5}}{4}$,
∴G′D=BD-GG′=$\frac{6\sqrt{10}}{5}$,
∵$\frac{{S}_{△PQD}}{{S}_{△PQG′}}$=$\frac{DQ}{QG′}$=$\frac{\frac{1}{2}•PD•QK}{\frac{1}{2}•PG′•QJ}$,
∵∠QPD=∠QPG′,QK⊥PD,QJ⊥PG′,
∴QK=QJ,
∴$\frac{DQ}{QG′}$=$\frac{PD}{PG′}$=2,
∴QD=$\frac{2}{3}$×$\frac{6\sqrt{10}}{5}$=$\frac{4\sqrt{10}}{5}$,
∴t=$\frac{QD}{2\sqrt{10}}$=$\frac{2}{5}$,
综上所述t=$\frac{2}{5}$ 或$\frac{2}{3}$秒时,△D′PQ与△PQB重叠部分的面积为△DPQ面积的$\frac{1}{2}$.
点评 本题考查二次函数综合题、一次函数、最小值问题、锐角三角函数、角平分线性质定理等知识,解题的关键是灵活运用这些知识,学会添加常用辅助线,学会利用面积法得到线段之间关系,学会利用对称解决最小值问题,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
| A. | 2x3•3x4=6x12 | B. | 4a2•3a3=12a5 | C. | 3m3•5m3=15m3 | D. | 4y•(2y3)2=8y7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在《实践与探究》活动中,小亮和小红分别用8个一样大小的长方形纸片拼图,小亮恰好拼成一个大的长方形,如图1所示,小红拼成如图2所示的正方形,但中间还留下一个边长为3cm的小正方形,请你通过计算,算出每个小长方形的面积是135cm2.
在《实践与探究》活动中,小亮和小红分别用8个一样大小的长方形纸片拼图,小亮恰好拼成一个大的长方形,如图1所示,小红拼成如图2所示的正方形,但中间还留下一个边长为3cm的小正方形,请你通过计算,算出每个小长方形的面积是135cm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com