
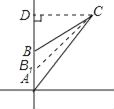
【题目】在军事上,常用时钟表示方向角(读数对应的时针方向),如正北为12点方向,北偏西30°为11点方向.在一次反恐演习中,甲队员在A处掩护,乙队员从A处沿12点方向以40米/分的速度前进,2分钟后到达B处.这时,甲队员发现在自己的1点方向的C处有恐怖分子,乙队员发现C处位于自己的2点方向(如图).假设距恐怖分子100米以外为安全位置.
(1)乙队员是否处于安全位置?为什么?
(2)因情况不明,甲队员立即发出指令,要求乙队员沿原路后撤,务必于15秒内到达安全位置.为此,乙队员至少应用多快的速度撤离?(结果精确到个位.参考数据:![]() ,
,![]() .)
.)

【答案】(1)乙队员不安全.(2)乙队员至少应以3米/秒的速度撤离.
【解析】(1)、根据题意得出AB=80,根据角度之间的关系得出BC=AB=80,从而得出答案;(2)、过点C作CD⊥AB,垂足为D,在AB边上取一点B1,使CB1=100米,根据Rt△CBD得出BD和CD的长度,根据Rt△CDB1中的勾股定理求出B1D的长度,从而得出BB1的长度.
解:(1)、乙队员不安全.易求AB=80米,∵∠DBC=60°,∠BAC=30°,
∴∠BCA=∠BAC=30°,∴BC=AB=80米<100米,∴乙队员不安全.
(2)、过点C作CD⊥AB,垂足为D,在AB边上取一点B1,使CB1=100米,
在Rt△CBD中,∠CBD=60°,BC=80米,则BD=40米,CD=40![]() 米,
米,
在Rt△CDB1中,由勾股定理知B1D=![]() =20
=20![]() 米,
米,
则BB1=(20![]() ﹣40)米,而
﹣40)米,而![]() ≈2.13(米/秒),
≈2.13(米/秒),
依题意结果精确到个位,所以乙队员至少应以3米/秒的速度撤离.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
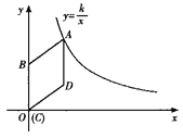
【题目】(8分)如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在函数y=![]() (k>0,x>0)的图象上,点D的坐标为(4,3).
(k>0,x>0)的图象上,点D的坐标为(4,3).
(1)求k的值;
(2)若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在函数y=![]() (k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
(k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)如图,四边形ABCD中,![]() ,E是边CD的中点,连接BE并延长与AD的延长线相较于点F.
,E是边CD的中点,连接BE并延长与AD的延长线相较于点F.

(1)求证:四边形BDFC是平行四边形;
(2)若△BCD是等腰三角形,求四边形BDFC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c图象对称轴是直线x=1,则下列结论:
①a<0,b<0,
②2a﹣b>0,
③a+b+c>0,
④a﹣b+c<0,
⑤当x>1时,y随x的增大而减小,
其中正确的是( )
A.①②③
B.②③④
C.③④⑤
D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:
(1)x2﹣2x﹣8=0;
(2)3x(x﹣1)=2(x﹣1);
(3)x2+3=3(x+1);
(4)2x(4x+5)=7;
(5)4x2﹣8x+1=0;
(6)(y+2)2=(3y﹣1)2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,![]() ,
,![]() 的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,
的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,![]() ,垂足为G,若
,垂足为G,若![]() ,则AE的边长为
,则AE的边长为![]()
![]()

A. ![]() B.
B. ![]() C. 4 D. 8
C. 4 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:
(1)x2﹣2x﹣8=0;
(2)3x(x﹣1)=2(x﹣1);
(3)x2+3=3(x+1);
(4)2x(4x+5)=7;
(5)4x2﹣8x+1=0;
(6)(y+2)2=(3y﹣1)2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+4x+3交x轴于A、B两点,(A在B左侧),交y轴于点C. 
(1)求A、B、C三点的坐标.
(2)求抛物线的对称轴及顶点坐标.
(3)抛物线上是否存在点F,使△ABF的面积为1?若存在,求F点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=4,∠ABC=30°,BC交⊙O于D,D是BC的中点. 
(1)求BC的长;
(2)过点D作DE⊥AC,垂足为E,求证:直线DE是⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com