
分析 (1)先把方程变形为(x-1)2=3,然后利用直接开平方法解方程;
(2)利用配方法得到(x-$\frac{5}{4}$)2=$\frac{9}{16}$,然后利用直接开平方法解方程;
(3)先把方程化为一般式得到2x2-7x-4=0,然后利用因式分解法解方程;
(4)先把方程变形为3x(x-2)-(x-2)=0,然后利用因式分解法解方程.
解答 解:(1)(x-1)2=3,
x-1=±$\sqrt{3}$,
所以x1=1+$\sqrt{3}$,x2=1-$\sqrt{3}$;
(2)x2-$\frac{5}{2}$x=1,
x2-$\frac{5}{2}$x+$\frac{25}{16}$=-1+$\frac{25}{16}$,
(x-$\frac{5}{4}$)2=$\frac{9}{16}$
x-$\frac{5}{4}$=±$\frac{3}{4}$,
所以x1=2,x2=$\frac{1}{2}$;
(3)2x2-7x-4=0,
(2x+1)(x-4)=0,
2x+1=0或x-4=0,
所以x1=-$\frac{1}{2}$,x2=4;
(4)3x(x-2)-(x-2)=0,
(x-2)(3x-1)=0,
x-2=0或3x-1=0,
所以x1=2,x2=$\frac{1}{3}$.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了直接开平方法和配方法解一元二次方程.


科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | -1 | D. | i |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
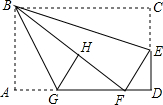 如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,①∠EBG=45°;②△DEF∽△ABG;③S△ABG=$\frac{3}{2}$S△FGH;④AG+DF=FG.则下列结论正确的有( )
如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,①∠EBG=45°;②△DEF∽△ABG;③S△ABG=$\frac{3}{2}$S△FGH;④AG+DF=FG.则下列结论正确的有( )| A. | ①②④ | B. | ①③④ | C. | ②③④ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
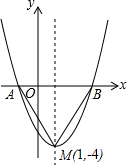 如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4),抛物线与x轴的交点为A、B(点A在点B的左边)
如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4),抛物线与x轴的交点为A、B(点A在点B的左边)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若a>0,b>0,则a+b>0 | B. | 若a<0,b<0,则a-b<0 | ||
| C. | 若a>0,b<0,且|a|>|b|,则a-b>0 | D. | 若a<0,b>0,且|a|>|b|,则a-b<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com