
分析 先求得x+y=2$\sqrt{5}$,xy=-2,
(1)利用完全平方公式变形,将x+y与xy的值代入计算即可求出值;
(2)首先把所求的式子变形成$\frac{(x+y)^{2}}{xy}$-2的形式,然后代入数值计算即可求解.
解答 解:∵x=$\sqrt{5}+\sqrt{7}$,y=$\sqrt{5}-\sqrt{7}$,
∴x+y=2$\sqrt{5}$,xy=-2,
(1)x2+y2=(x+y) 2-2xy=(2$\sqrt{5}$)2-2×(-2)=24;
(2)$\frac{y}{x}+\frac{x}{y}$=$\frac{(x+y)^{2}}{xy}$-2=$\frac{20}{-2}$-2=-12.
点评 本题考查了二次根式的化简求值,正确对所求的式子进行变形是关键.


科目:初中数学 来源: 题型:解答题
 如图,在正方形ABCD中,点E是AD上的点,点F是BC的延长线上一点,CF=DE,连结BE和EF,EF与CD交于点G,且∠FBE=∠FEB.
如图,在正方形ABCD中,点E是AD上的点,点F是BC的延长线上一点,CF=DE,连结BE和EF,EF与CD交于点G,且∠FBE=∠FEB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
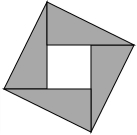 2002年8月在北京召开的国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a,较短直角边为b,则(a+b)2的值为( )
2002年8月在北京召开的国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a,较短直角边为b,则(a+b)2的值为( )| A. | 25 | B. | 19 | C. | 13 | D. | 169 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
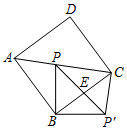 如图,正方形ABCD的边长是7$\sqrt{2}$,点P是对角线AC上的一个点(不与A,C两点重合),连接BP,并将线段BP绕点B顺时针旋转90°得到线段BP′,连接PP′,CP′,PP′与BC相交于点E.
如图,正方形ABCD的边长是7$\sqrt{2}$,点P是对角线AC上的一个点(不与A,C两点重合),连接BP,并将线段BP绕点B顺时针旋转90°得到线段BP′,连接PP′,CP′,PP′与BC相交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 5 | C. | 7 | D. | 无数个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}a+b=1\\ 2a+b=4\end{array}\right.$ | B. | $\left\{\begin{array}{l}3a+b=3\\ 2a+b=4\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}a+b=1\\ 3a-2c=19\end{array}\right.$ | D. | $\left\{\begin{array}{l}5a-2b=19\\ 3a+b=3\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一次右拐60°,第二次左拐120° | B. | 第一次左拐60°,第二次右拐60° | ||
| C. | 第一次左拐60°,第二次左拐120° | D. | 第一次右拐60°,第二次右拐60° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com