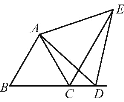
【题目】如图,点B,C,D在一条直线上,△ABC,△ADE是等边三角形,若CE=15cm,CD=6cm,则AC=__,∠ECD=__.
【答案】9cm； 60.
【解析】
根据等边三角形性质得出AB=AC，AD=AE，∠BAC=∠EAD=∠B=60°，求出∠BAD=∠CAE，根据SAS证△BAD≌△CAE，推出∠ACE=∠B=60°，BD=CE=15cm，求出BC和∠ECD即可．
解：∵△ABC、△ADE是等边三角形，
∴AB=AC，AD=AE，∠BAC=∠EAD=∠B=60°，
∴∠BAC+∠CAD=∠EAD+∠CAD，
即∠BAD=∠CAE，
∵在△BAD和△CAE中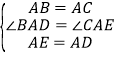
，
∴△BAD≌△CAE（SAS），
∴∠ACE=∠B=60°，BD=CE=15cm，
∴BC=BD-CD=15cm-6cm=9cm，
∵△ABC是等边三角形，
∴AC=BC=9cm，
∵∠B+∠BAC=∠ACD=120°，∠ACE=∠B=60°，
∴∠ECD=60°，
故答案为：9cm，60.
科目：初中数学 来源： 题型：
【题目】已知△ABC中，∠BAC＝90°，AB＝AC．
（1）如图，D为AC上任一点，连接BD，过A点作BD的垂线交过C点与AB平行的直线CE于点E．求证：BD＝AE．
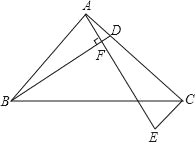
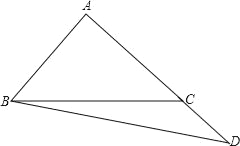
（2）若点D在AC的延长线上，如图，其他条件同（1），请画出此时的图形，并猜想BD与AE是否仍然相等？说明你的理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1是一个长为
、宽为
的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成一个“回形”正方形（如图2）
（1）观察图2请你写出
、
、
之间的等量关系是______；
（2）根据（1）中的结论，若
，
，则
______；
（3）拓展应用：若
，求
的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是由九个等边三角形组成的一个六边形,当最小的等边三角形边长为2 cm时,这个六边形的周长为
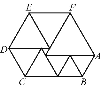
A. 30cm B. 40cm C. 50cm D. 60cm
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在Rt△ABC中，∠ACB=90°，∠A=30°，BD是△ABC的角平分线，DE⊥AB于点E．
（1）如图1，连接EC，求证：△EBC是等边三角形；
（2）点M是线段CD上的一点（不与点C，D重合），以BM为一边，在BM的下方作∠BMG=60°，MG交DE延长线于点G．请你在图2中画出完整图形，并直接写出MD，DG与AD之间的数量关系；
（3）如图3，点N是线段AD上的一点，以BN为一边，在BN的下方作∠BNG=60°，NG交DE延长线于点G．试探究ND，DG与AD数量之间的关系，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】郴州市正在创建“全国文明城市”，某校拟举办“创文知识”抢答赛，欲购买A、B两种奖品以鼓励抢答者．如果购买A种20件，B种15件，共需380元；如果购买A种15件，B种10件，共需280元．
（1）A、B两种奖品每件各多少元？
（2）现要购买A、B两种奖品共100件，总费用不超过900元，那么A种奖品最多购买多少件？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示的运算程序中，若开始输入的x值为7，我们发现第1次输出的结果为10，第2次输出的结果为5，……，第2019次输出的结果为_____．
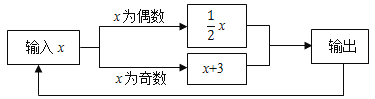
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】推理填空：
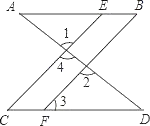
如图，已知∠1＝∠2，∠B＝∠C，可推得AB∥CD．理由如下：
∵∠1＝∠2（已知），且∠1＝∠4（ ）
∴∠2＝∠4 （等量代换）
∴CE∥BF （ ）
∴∠ ＝∠3（ ）
又∵∠B＝∠C（已知），∴∠3＝∠B（等量代换）
∴AB∥CD （ ）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知AB∥CD，EF交AB于E，交CD于F，∠AEF＝68°，FG平分∠EFD，KF⊥FG，求∠KFC的度数.
解：∵AB∥CD(已知)
∴∠EFD＝∠AEF( )
∵∠AEF＝68°(已知)
∴∠EFD＝∠AEF＝68°( )
∵FG平分∠EFD(已知)
所以∠EFG＝∠GFD＝
∠EFD＝34°( )
又因为KF⊥FG( )
所以∠KFG＝90°( )
所以∠KFC＝180°－∠GFD－∠KFG＝ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com