
【题目】如图,在四边形ABCD中,AB//CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE .
(1)求证:四边形ABCD是平行四边形;
(2)若点E是AC的中点,判断BE与AC的位置关系,并说明理由;
(3)若△ABE是等边三角形,AD=![]() ,求对角线AC的长 .
,求对角线AC的长 .
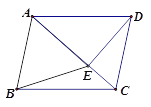
【答案】(1)证明见解析;(2)BE⊥AC,理由见解析;(3)AC=![]()
【解析】试题分析:(1)根据平行四边形的性质得出∠ABC+∠DCB=180°,推出∠ADC+∠BCD=180°,根据平行线的判定得出AD∥BC,根据平行四边形的判定推出即可;(2)求出AD=DC,根据菱形的判定得出四边形ABCD是菱形,根据等腰三角形的性质得出即可;(3)根据等边三角形的性质得出AB=AE,∠BAC=60°,求出∠DCE=∠BAE=60°,求出CD=2EC,设CE=x,则AB=DC=AE=2x,根据勾股定理得出方程,求出x,即可得出答案.
试题解析:(1) 证明:∵AB∥CD
∴∠ABC+∠BCD=180°,
∠ADC+∠BAD=180°,
又∵∠ABC =∠ADC,
∴∠BAD=∠BCD,
∴四边形ABCD是平行四边形.
(2)∵DE⊥AC,且E是AC的中点,
∴ AD=DC .
由(1)可得四边形ABCD是平行四边形
∴ 四边形 ABCD是菱形.
∴ AB=BC
∵ E是AC中点,
∴ BE⊥AC.
(3)在平行四边形ABCD中,AB∥CD
∵△ABE是等边三角形
∴ ∠BAE=60°
∴ ∠ACD=60°
∵ DE⊥AC
∴ ∠DEC=90°,
∴ ∠EDC=30° ,
∴ EC=![]() DC
DC
设EC=x,则DC=2x
∴ DE=![]() , AB=AE=2x ,
, AB=AE=2x ,
在Rt△ADE中,
AE2+OE2=AD2
∴![]() , 解得
, 解得 ![]() ,
,
∴AC=3![]() .
.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有4个黑球、2个白球,每个球除颜色外都相同,从中任意摸出3个球,下列事件为必然事件的是( )
A.至少有1个球是黑球
B.至少有1个球是白球
C.至少有2个球是黑球
D.至少有2个球是白球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的B'点,AE是折痕。

(1)试判断B'E与DC的位置关系并说明理由。
(2)如果∠C=130°,求∠AEB的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的∠ABC和∠ACB的平分线BE,CF交于点G,若∠BGC=115°,则∠A= .
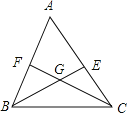
【答案】50°
【解析】
试题分析:根据三角形内角和定理求出∠GBC+∠GCB,根据角平分线的定义求出∠ABC+∠ACB,根据三角形内角和定理计算即可.
解:∵∠BGC=115°,
∴∠GBC+∠GCB=180°﹣115°=65°,
∵BE,CF是△ABC的∠ABC和∠ACB的平分线,
∴∠GBC=![]() ABC,∠GCB=
ABC,∠GCB=![]() ACB,
ACB,
∴∠ABC+∠ACB=130°,
∴∠A=180°﹣130°=50°,
故答案为:50°.
【题型】填空题
【结束】
14
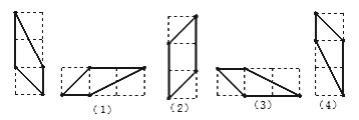
【题目】如图所示,有(1)~(4)4个条形方格图,图中由实线围成的图形与前图全等的有
________(只要填序号即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,E,D是AB,AC上的两点,BD,CE交于点O,且AB=AC,使△ACE≌△ABD,你补充的条件是________
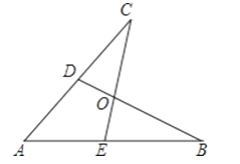
【答案】AD=AE或CD=BE或∠B=∠C或∠ADB=∠AEC
【解析】AD=AE或CD=BE或∠B=∠C或∠ADB=∠AEC;理由如下:
若AD=AE,
在△ACE和△ABD中, 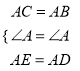 ,
,
∴△ACE≌△ABD(SAS);
若CD=BE,
∵AB=AC,
∴AD=AE,
同理:△ACE≌△ABD(SAS);
若∠B=∠C,
在△ACE和△ABD中, 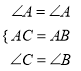 ,
,
∴△ACE≌△ABD(ASA);
若∠ADB=∠AEC,
在△ACE和△ABD中, 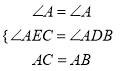 ,
,
∴△ACE≌△ABD(AAS);
故答案为:AD=AE或CD=BE或∠B=∠C或∠ADB=∠AEC.
点睛:本题考查了全等三角形的判定方法,是开放型题目,存在四种情况,熟练掌握全等三角形的判定方法是解决问题的关键.
【题型】填空题
【结束】
17
【题目】如图,四边形ABCD与四边形A′B′C′D′全等,则∠A′=________,∠A=________,B′C′=________,AD=________.
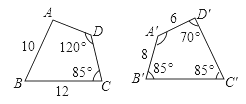
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下调查中,应采用全面调查的是( )
A.调查某批次汽车的抗撞击能力
B.了解全国中学生的视力和用眼卫生情况
C.了解某班学生的身高情况
D.调查某池塘中现有鱼的数量
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com