
分析 根据根与系数的关系得出“m+n=2,mn=-1”,再将3m2-n2-8m+1变形为只含m+n与mn的代数式,代入数据即可得出结论.
解答 解:∵m、n是关于x的一元二次方程x2-2x-1=0的两个实数根,
∴m+n=-$\frac{b}{a}$=2,mn=$\frac{c}{a}$=-1.
∴3m2-n2-8m+1=(4m2-8m)-(m2+n2)+1=-4mn-[(m+n)2-2mn]+1=4-6+1=-1.
故答案为:-1.
点评 本题考查了根与系数的关系,解题的关键是找出3m2-n2-8m+1=-4mn-[(m+n)2-2mn]+1.本题属于基础题,难度不大,解决该题型题目时,根据根与系数的关系找出两根之和与两根之积,再将代数式变形为只含两根之和与两根之积的形式是关键.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
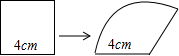 手工课上,小明将一个边长为4cm的正方形铁丝框,变形成为如图所示一个扇形框,周长不变,且扇形框半径等于正方形的边长,则该扇形的面积大小为16cm2.
手工课上,小明将一个边长为4cm的正方形铁丝框,变形成为如图所示一个扇形框,周长不变,且扇形框半径等于正方形的边长,则该扇形的面积大小为16cm2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1-(1-x)=1 | B. | 1+(1-x)=1 | C. | 1-(1-x)=x-2 | D. | 1+(1-x)=x-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
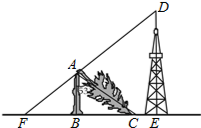 如图,一棵大树在一次强台风中折断倒下,未折断树杆AB与地面仍保持垂直的关系,而折断部分AC与未折断树杆AB形成53°的夹角.树杆AB旁有一座与地面垂直的铁塔DE,测得BE=6米,塔高DE=9米.在某一时刻的太阳照射下,未折断树杆AB落在地面的影子FB长为4米,且点F、B、C、E在同一条直线上,点F、A、D也在同一条直线上.求这棵大树没有折断前的高度.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33)
如图,一棵大树在一次强台风中折断倒下,未折断树杆AB与地面仍保持垂直的关系,而折断部分AC与未折断树杆AB形成53°的夹角.树杆AB旁有一座与地面垂直的铁塔DE,测得BE=6米,塔高DE=9米.在某一时刻的太阳照射下,未折断树杆AB落在地面的影子FB长为4米,且点F、B、C、E在同一条直线上,点F、A、D也在同一条直线上.求这棵大树没有折断前的高度.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com