
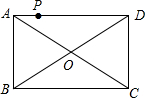
 如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是$\frac{24}{5}$.
如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是$\frac{24}{5}$. 分析 首先连接OP,由矩形的两条边AB、BC的长分别为6和8,可求得OA=OD=5,△AOD的面积,然后由S△AOD=S△AOP+S△DOP=$\frac{1}{2}$OA•PE+OD•PF求得答案.
解答 解:解:连接OP,
∵矩形的两条边AB、BC的长分别为6和8,
∴S矩形ABCD=AB•BC=48,OA=OC,OB=OD,AC=BD=10,
∴OA=OD=5,
∴S△ACD=$\frac{1}{2}$S矩形ABCD=24,
∴S△AOD=$\frac{1}{2}$S△ACD=12,
∵S△AOD=S△AOP+S△DOP=$\frac{1}{2}$OA•PE+$\frac{1}{2}$OD•PF=$\frac{1}{2}$×5×PE+$\frac{1}{2}$×5×PF=$\frac{5}{2}$(PE+PF)=12,
解得:PE+PF=$\frac{24}{5}$,
故答案为$\frac{24}{5}$
点评 此题考查了矩形的性质以及三角形面积问题.此题难度适中,注意掌握辅助线的作法以及掌握整体数学思想的运用是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | -3x<-3y | B. | 3x>3y | C. | $\frac{x}{2}$<$\frac{y}{2}$ | D. | -x-2<-y-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 相等的两个角是对顶角 | |
| B. | 三角形的一个外角等于它的两个内角和 | |
| C. | 互补的两个角不一定相等 | |
| D. | 有一个角对应相等的两个等腰三角形是全等三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
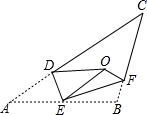 如图,△ABC中,点E是AB中点,点D、F分别在AC、BC上,将△AED、△BEF分别沿ED、EF翻折,使顶点A、B都落在点O处,若∠CDO+∠CFO=98°,则∠C的度数( )
如图,△ABC中,点E是AB中点,点D、F分别在AC、BC上,将△AED、△BEF分别沿ED、EF翻折,使顶点A、B都落在点O处,若∠CDO+∠CFO=98°,则∠C的度数( )| A. | 40° | B. | 41° | C. | 42° | D. | 43° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
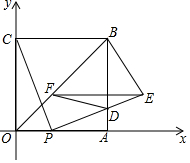 如图,四边形OABC是边长为4的正方形,点P从点O沿边OA向点A运动,每秒运动1个单位.连结CP,过点P作PE⊥CP交AB于点D,且PE=PC,过点E作EF∥OA,交OB于点F,连结FD、BE,设点P运动的时间为t(0<t<4).
如图,四边形OABC是边长为4的正方形,点P从点O沿边OA向点A运动,每秒运动1个单位.连结CP,过点P作PE⊥CP交AB于点D,且PE=PC,过点E作EF∥OA,交OB于点F,连结FD、BE,设点P运动的时间为t(0<t<4).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
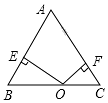 如图,△ABC是等腰三角形,点O 是底边BC上任意一点,OE、OF分别与两边垂直,等腰三角形的腰长为5,面积为12,则OE+OF的值为( )
如图,△ABC是等腰三角形,点O 是底边BC上任意一点,OE、OF分别与两边垂直,等腰三角形的腰长为5,面积为12,则OE+OF的值为( )| A. | 4 | B. | $\frac{24}{5}$ | C. | 15 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com