
【题目】如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,-3),动点P在抛物线上.
(1)b =_________,c =_________,点B的坐标为_____________;(直接填写结果)
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
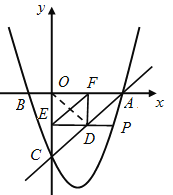
(3)过动点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.

【答案】(1)![]() ,
, ![]() ,
, ![]() (2)存在P的坐标是
(2)存在P的坐标是![]() 或
或![]() (3)当EF最短时,点P的坐标是:(
(3)当EF最短时,点P的坐标是:(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() )
)
【解析】试题分析:(1)根据题意得出答案;(2)分以点C为直角顶点和点A为直角顶点两种情况分别进行计算;两种情况都根据等腰直角三角形的性质得出点的坐标;(3)根据垂线段最短,可得当OD⊥AC时,OD最短,即EF最短,根据OC=OA=3,OD⊥AC得出 D是AC的中点,从而得出点P的纵坐标,然后根据题意得出方程,从而求出点P的坐标.
试题解析:(1)![]() ,
,![]() , (-1,0).
, (-1,0).
(2)存在.
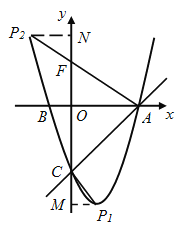
第一种情况,当以C为直角顶点时,过点C作CP1⊥AC,交抛物线于点P1.过点P1作y轴的垂线,垂足是M.
∵OA=OC,∠AOC =90° ∴∠OCA=∠OAC=45°. ∵∠ACP1=90°, ∴∠MCP1=90°-45°=45°=∠C P1M.
∴MC=MP1. 由(1)可得抛物线为![]() .
.
设![]() ,则
,则![]() , 解得:
, 解得:![]() (舍去),
(舍去),![]() .
.
∴![]() . 则P1的坐标是
. 则P1的坐标是![]() .
.
第二种情况,当以A为直角顶点时,过点A作AP2⊥AC,交抛物线于点P2,过点P2作y轴的垂线,垂足是N,AP2交y轴于点F. ∴P2N∥x轴.由∠CAO=45°, ∴∠OAP2=45°. ∴∠FP2N=45°,AO=OF=3.
∴P2N=NF. 设![]() ,则
,则![]() . 解得:
. 解得:![]() (舍去),
(舍去),![]() .
.
∴![]() , 则P2的坐标是
, 则P2的坐标是![]() .
.
综上所述,P的坐标是![]() 或
或![]()
(3)连接OD,由题意可知,四边形OFDE是矩形,则OD=EF.
根据垂线段最短,可得当OD⊥AC时,OD最短,即EF最短. 由(1)可知,在Rt△AOC中,
∵OC=OA=3,OD⊥AC, ∴ D是AC的中点. 又∵DF∥OC, ∴![]() .
.
∴点P的纵坐标是![]() 则
则![]() , 解得:
, 解得:![]() .
.
∴当EF最短时,点P的坐标是:(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】第十三届国际动漫节近日在杭州闭幕,共吸引了来自82个国家和地区的1394500人参与,将数据1394500用科学记数法表示为( )
A.1.3945×104
B.13.945×105
C.1.3945×106
D.1.3945×108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某校开展的“书香校园”读书活动中,学校为了解八年级学生的读书情况,随机调查了八年级50名学生每学期每人读书的册数,绘制统计表如下:
册数 | 0 | 1 | 2 | 3 | 4 |
人数 | 4 | 12 | 16 | 17 | 1 |
则这50个样本数据的众数和中位数分别是( )
A.17,16
B.3,2.5
C.2,3
D.3,2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列说法:①△ABC在平移的过程中,对应线段一定相等.②△ABC在平移的过程中,对应线段一定平行.③△ABC在平移的过程中,周长不变.④△ABC在平移的过程中,面积不变.其中正确的有( )
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com