
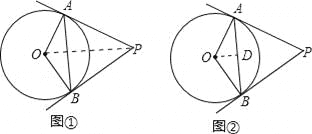
【题目】如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30°.
(1)求∠APB的度数;
(2)当OA=3时,求AP的长.

【答案】(1)60°;(2)![]() .
.
【解析】
试题(1)、方法1,根据四边形的内角和为360°,根据切线的性质可知:∠OAP=∠OBP=90°,求出∠AOB的度数,可将∠APB的度数求出;方法2,证明△ABP为等边三角形,从而可将∠APB的度数求出;
(2)、方法1,作辅助线,连接OP,在Rt△OAP中,利用三角函数,可将AP的长求出;方法2,作辅助线,过点O作OD⊥AB于点D,在Rt△OAD中,将AD的长求出,从而将AB的长求出,也即AP的长.
试题解析:(1)、方法一: ∵在△ABO中,OA=OB,∠OAB=30°, ∴∠AOB=180°﹣2×30°=120°,
∵PA、PB是⊙O的切线, ∴OA⊥PA,OB⊥PB,即∠OAP=∠OBP=90°, ∴在四边形OAPB中,
∠APB=360°﹣120°﹣90°﹣90°=60°.
方法二: ∵PA、PB是⊙O的切线∴PA=PB,OA⊥PA;
∵∠OAB=30°,OA⊥PA, ∴∠BAP=90°﹣30°=60°, ∴△ABP是等边三角形, ∴∠APB=60°.
(2)、方法一:如图①,连接OP; ∵PA、PB是⊙O的切线,∴PO平分∠APB,即∠APO=![]() ∠APB=30°,
∠APB=30°,
又∵在Rt△OAP中,OA=3,∠APO=30°, ∴AP=![]() =3
=3![]() .
.
方法二:如图②,作OD⊥AB交AB于点D; ∵在△OAB中,OA=OB, ∴AD=![]() AB;
AB;
∵在Rt△AOD中,OA=3,∠OAD=30° ∴AD=OAcos30°=![]() , ∴AP=AB=3
, ∴AP=AB=3![]() .
.


科目:初中数学 来源: 题型:
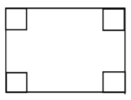
【题目】如图,一块长和宽分别为30cm和20cm的矩形铁皮,要在它的四角截去四个边长相等的小正方形,折成一个无盖的长方体盒子,使它的侧面积为272cm2,则截去的正方形的边长是( )cm
A.4cmB.8.5cmC.4cm或8.5cmD.5cm或7.5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E,F分别是锐角∠A两边上的点,AE=AF,分别以点E,F为圆心,以AE的长为半径画弧,两弧相交于点D,连接DE,DF.
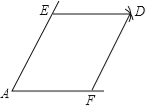
(1)请你判断所画四边形的性状,并说明理由;
(2)连接EF,若AE=8厘米,∠A=60°,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
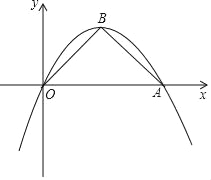
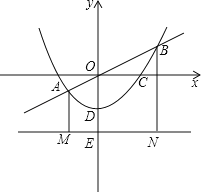
【题目】如图,在平面直角坐标系xOy,已知二次函数y=﹣![]() x2+bx的图象过点A(4,0),顶点为B,连接AB、BO.
x2+bx的图象过点A(4,0),顶点为B,连接AB、BO.
(1)求二次函数的表达式;
(2)若C是BO的中点,点Q在线段AB上,设点B关于直线CQ的对称点为B',当△OCB'为等边三角形时,求BQ的长度;
(3)若点D在线段BO上,OD=2DB,点E、F在△OAB的边上,且满足△DOF与△DEF全等,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=x2﹣3x+2和一次函数y=﹣2x+4,把y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线L.现有点A(2,0)和抛物线L上的点B(﹣1,n),请完成下列任务:
(尝试)
(1)当t=2时,抛物线y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)的顶点坐标为 ;
(2)判断点A是否在抛物线L上;
(3)求n的值;
(发现)
通过(2)和(3)的演算可知,对于t取任何不为零的实数,抛物线L总过定点,坐标为 .
(应用)
二次函数y=﹣3x2+5x+2是二次函数y=x2﹣3x+2和一次函数y=﹣2x+4的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAP是等腰直角三角形,∠OAP=90°,点A在第四象限,点P坐标为(8,0),抛物线y=ax2+bx+c经过原点O和A、P两点.

(1)求抛物线的函数关系式.
(2)点B是y轴正半轴上一点,连接AB,过点B作AB的垂线交抛物线于C、D两点,且BC=AB,求点B坐标;
(3)在(2)的条件下,点M是线段BC上一点,过点M作x轴的垂线交抛物线于点N,求△CBN面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国高铁近年来用震惊世界的速度不断发展,已成为当代中国一张耀眼的“国家名片”。修建高铁时常常要逢山开道、遇水搭桥。如图,某高铁在修建时需打通一直线隧道MN(M、N为山的两侧),工程人员为了计算MN两点之间的直线距离,选择了在测量点A、B、C进行测量,点B、C分别在AM、AN上,现测得AM=1200米,AN=2000米,AB=30米,BC=45米,AC=18米,求直线隧道MN的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
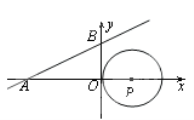
【题目】如图,直线y=![]() x+
x+![]() 与x轴、y轴分别相交于A、B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左移动,当⊙P与该直线相交时,满足横坐标为整数的点P的个数是( )
与x轴、y轴分别相交于A、B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左移动,当⊙P与该直线相交时,满足横坐标为整数的点P的个数是( )
A.3B.4C.5D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com