
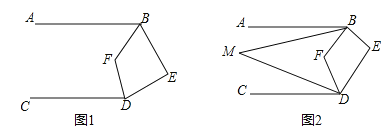
【题目】如图:已知AB∥CD,∠ABE与∠CDE两个角的角平分线相交于F.
(1)如图1,若∠E=80°,求∠BFD的度数.
(2)如图2:若∠ABM=![]() ∠ABF,∠CDM=
∠ABF,∠CDM=![]() ∠CDF,写出∠M和∠E之间的数量关系并证明你的结论.
∠CDF,写出∠M和∠E之间的数量关系并证明你的结论.
(3)若∠ABM=![]() ∠ABF, ∠CDM=
∠ABF, ∠CDM=![]() ∠CDF, 设∠E=m°,直接用含有n、m°的代数式写出∠M= (不写过程)
∠CDF, 设∠E=m°,直接用含有n、m°的代数式写出∠M= (不写过程)
【答案】(1)140°;(2)6∠M+∠E=360°.(3)![]()
【解析】试题分析:(1)首先作EG∥AB,FH∥AB,利用平行线的性质可得∠ABE+∠CDE=280°,再利用角平分线的定义得到∠ABF+∠CDF=140°,从而得到∠BFD的度数;(2)先由已知得到∠ABE=6∠ABM,∠CDE=6∠CDM,由(1)得∠ABE+∠CDE=360°﹣∠E,∠M=∠ABM+∠CDM,等量代换,即可;
(3)由(2)的方法可得到2n∠M+∠E=360°,将∠E=m°代入可得![]() .
.
解:(1)作EG∥AB,FH∥AB,
∵AB∥CD,
∴EG∥AB∥FH∥CD,
∴∠ABF=∠BFH,∠CDF=∠DFH,∠ABE+∠BEG=180°,∠GED+∠CDE=180°,
∴∠ABE+∠BEG+∠GED+∠CDE=360°
∵∠BED=∠BEG+∠DEG=80°,
∴∠ABE+∠CDE=280°,
∵∠ABF和∠CDF的角平分线相交于E,
∴∠ABF+∠CDF=140°,
∴∠BFD=∠BFH+∠DFH=140°;
(2)∵∠ABM=∠ABF,∠CDM=∠CDF,
∴∠ABF=3∠ABM,∠CDF=3∠CDM,
∵∠ABE与∠CDE两个角的角平分线相交于点F,
∴∠ABE=6∠ABM,∠CDE=6∠CDM,
∴6∠ABM+6∠CDM+∠E=360°,
∵∠M=∠ABM+∠CDM,
∴6∠M+∠E=360°.
(3)由(2)结论可得,
2n∠ABN+2n∠CDM+∠E=360°,∠M=∠ABM+∠CDM,
解得:![]() .
.
故答案为:![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
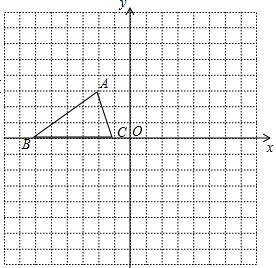
(1)请直接写出点A关于y轴对称的点的坐标:______
(2)将△ABC绕坐标原点O逆时针旋转90°.画出图形,直接写出点B的对应点的坐标:___________
(3)请直接写出以A、B、C为顶点的平行四边形的第四个顶点D的坐标:____________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列式子可利用x2+(p+q)x+pq=(x+p)(x+q)分解因式的是( )
A. x2﹣3x+2 B. 3x2﹣2x+1 C. x2+x+3 D. 3x2+5x+7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com