
分析 先将第n个数化简,再将n=10和n=11分别代入计算第10个数、第11个数即可.
解答 解:第n个数:$\frac{1}{n+1}$-(1+$\frac{-1}{2}$)[1+$\frac{(-1)^{2}}{3}$][1+$\frac{(-1)^{3}}{4}$]•[1+$\frac{(-1)^{4}}{5}$]…[1+$\frac{(-1)^{2n-1}}{2n}$],
=$\frac{1}{n+1}$-$\frac{1}{2}$×$\frac{4}{3}$×$\frac{3}{4}$×$\frac{6}{5}$×$\frac{5}{6}$×…×$\frac{2n}{2n-1}$×$\frac{2n-1}{2n}$,
=$\frac{1}{n+1}$-$\frac{1}{2}$,
∴第10个数是:$\frac{1}{11}$-$\frac{1}{2}$=-$\frac{9}{22}$,
第11个数是:$\frac{1}{12}$-$\frac{1}{2}$=-$\frac{5}{12}$,
则:第10个数是-$\frac{9}{22}$、第11个数是-$\frac{5}{12}$,第n个数是$\frac{1}{n+1}$-$\frac{1}{2}$.
点评 本题是数字类的变化规律题,主要考查了根据规律求解问题,可以将通式化简到最简情况,作为公式代入计算.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | (a3)3=a3+3=a6 | B. | [(b2)2]2=b2×3=b6 | C. | (-y2)3=y6 | D. | [(-x)3]2=(-x)6=x6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
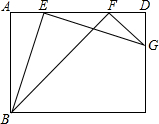 如图,在矩形ABCD中,∠BEG=∠BFG=90°,AB=AF.
如图,在矩形ABCD中,∠BEG=∠BFG=90°,AB=AF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com