
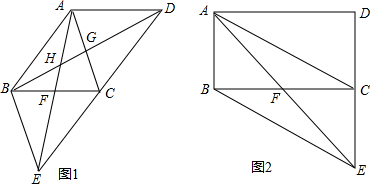
���� ��1������ƽ���ı��ε����ʵó�AB��DE��֤���ı���ABEC��ƽ���ı��Σ����BC=2AB�����ɵó��ı���ABEC�������ı��Σ�
�ڵ�AC=2CDʱ���ı���ABCD�������ı��Σ���ʱAD=m=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$����AC=2ADʱ���ı���ABCD�������ı��Σ��ɹ��ɶ����ó�����m2+12=��2m��2���ⷽ�̼��ɣ�
��2���������ı��εĶ���ó�AD=DG���ó���DAG=��AGD��ͬ��AC=AF���ó���ACF=��AFC��֤����ADG=��CAF��$\frac{AD}{BD}$=$\frac{AC}{AE}$���ó���ADB�ס�ACE����AB=CE���ó���ADB�ա�ACE����ȫ�������ε����ʵó�AC=AD����DM��AC��M����AM=x����AC=AD=4x���ɹ��ɶ����ã�DM=$\sqrt{15}$x��CD=2$\sqrt{6}$x����CD=AB=1�ó����̣��ⷽ�̼��ɣ�
��� ��1����֤�������ı���ABCD��ƽ���ı��Σ�
��AB��DE��
��BE��AC��
���ı���ABEC��ƽ���ı��Σ�
��AB=1��BC=m=2��
��BC=2AB��
���ı���ABEC�������ı��Σ�
�ڽ⣺���ڣ��������£�
��AC=2CDʱ���ı���ABCD�������ı��Σ���ʱAD=m=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$��
��AC=2ADʱ���ı���ABCD�������ı��Σ�
����m2+12=��2m��2��
��ã�m=��$\frac{\sqrt{3}}{3}$����ֵ��ȥ����
��m=$\frac{\sqrt{3}}{3}$��
��m��ֵΪ$\sqrt{3}$��$\frac{\sqrt{3}}{3}$ʱ���ı���ABCD�������ı��Σ�
��2���⣺���ı���ABCD�������ı��Σ�BDΪ�����Խ��ߣ�ADΪ�����ߣ�
��AD=DG��
���DAG=��AGD��
���ı���ABEC�������ı��Σ�AEΪ�����Խ��ߣ�ACΪ�����ߣ�
��AC=AF��
���ACF=��AFC��
�֡ߡ�DAG=��ACF��
���DAG=��AGD=��ACF=��AFC��
���ADG=��CAF��
�֡�$\frac{AD}{BD}$=$\frac{1}{2}$��$\frac{AC}{AE}$=$\frac{1}{2}$��
��$\frac{AD}{BD}$=$\frac{AC}{AE}$��
���ADB�ס�ACE��
�֡�AB=CE��
�����Ʊ�Ϊ1��
���ADB�ա�ACE��
��AC=AD��
��DM��AC��M����ͼ1��ʾ��
��AM=x����AC=AD=4x��
��Rt��ADM�У��ɹ��ɶ����ã�DM=$\sqrt{15}$x��
��Rt��DMC�У��ɹ��ɶ����ã�CD=2$\sqrt{6}$x��
��CD=AB=1��
��2$\sqrt{6}$x=1��
��x=$\frac{\sqrt{6}}{12}$��
��AD=4x=$\frac{\sqrt{6}}{3}$��
��m=$\frac{\sqrt{6}}{3}$��
���� �������ı����ۺ���Ŀ��������ƽ���ı��ε����ʡ������ı��ε��ж������ʡ����ɶ��������������ε��ж������ʵ�֪ʶ�������ۺ���ǿ����һ���Ѷȣ�


 �Ƹ�С״Ԫ�������������ϵ�д�
�Ƹ�С״Ԫ�������������ϵ�д� ����һ������ܼƻ�ϵ�д�
����һ������ܼƻ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������OAB�У���AOB=90�㣬�뾶OA=2$\sqrt{3}$��������OAB�ع���B��ֱ���۵�����Oǡ������$\widehat{AB}$�ϵĵ�D�����ۺ۽�OA�ڵ�C������Ӱ���ֵ������3��-4$\sqrt{3}$��
��ͼ��������OAB�У���AOB=90�㣬�뾶OA=2$\sqrt{3}$��������OAB�ع���B��ֱ���۵�����Oǡ������$\widehat{AB}$�ϵĵ�D�����ۺ۽�OA�ڵ�C������Ӱ���ֵ������3��-4$\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
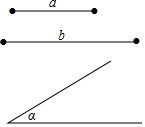 ��֪���߶�a��b���Ϧ�����ͼ������ֱ�ߺ�Բ����һ��ƽ���ı��Σ�ʹ���������Խ��߳��ֱ�����߶�a��b���������Խ������ɵ�һ���ǵ��ڡϦ���
��֪���߶�a��b���Ϧ�����ͼ������ֱ�ߺ�Բ����һ��ƽ���ı��Σ�ʹ���������Խ��߳��ֱ�����߶�a��b���������Խ������ɵ�һ���ǵ��ڡϦ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
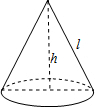 ��ͼ��һ��Բ���̴�Сֽñ������ĸ�߳�l��13cm����hΪ12cm���������ⶥֽñ����ֽ�ŵ�����ǣ��ӷ���Բ��ƣ���������
��ͼ��һ��Բ���̴�Сֽñ������ĸ�߳�l��13cm����hΪ12cm���������ⶥֽñ����ֽ�ŵ�����ǣ��ӷ���Բ��ƣ���������| A�� | 60�� | B�� | 65�� | C�� | 78�� | D�� | 156�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | |a|+|b| | B�� | |a|-|b| | C�� | |a+b| | D�� | |a-b| |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
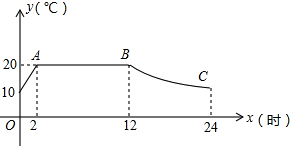
 �����ͽγ�ͬʱ��A���ر�ֱ�Ĺ�·ȥB�أ��γ���B��ͣ��һ��ʱ���ԭ·ԭ�ٷ��أ�����������ǰ������֮��ľ���y��km���������뿪A�ص�ʱ��t��h��֮��ĺ�����ϵ��ͼ��ʾ������������ʱ��ʱ��Ϊ��������
�����ͽγ�ͬʱ��A���ر�ֱ�Ĺ�·ȥB�أ��γ���B��ͣ��һ��ʱ���ԭ·ԭ�ٷ��أ�����������ǰ������֮��ľ���y��km���������뿪A�ص�ʱ��t��h��֮��ĺ�����ϵ��ͼ��ʾ������������ʱ��ʱ��Ϊ��������| A�� | 3.25h | B�� | 3.50h | C�� | 3.75h | D�� | 4h |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
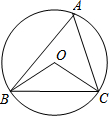 ��ͼ����ABC�ǡ�O���ڽ������Σ�����OB��OC������BAC+��BOC=180�㣬BC=2$\sqrt{3}$cm�����O�İ뾶Ϊ2cm��
��ͼ����ABC�ǡ�O���ڽ������Σ�����OB��OC������BAC+��BOC=180�㣬BC=2$\sqrt{3}$cm�����O�İ뾶Ϊ2cm���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com