
【题目】如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.求证:(1)△ADE≌△BEC (2)△CDE 是直角三角形 .

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
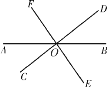
【题目】如图,直线AB,CD,EF相交于点O,则∠AOD的对顶角是_________,∠AOC的邻补角是_______.若∠AOC=50°,则∠BOD=__________,∠COB=______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(﹣3,4),点C在![]() 轴的正半轴上,直线AC交
轴的正半轴上,直线AC交![]() 轴于点M,AB边交y轴于点H,连接BM.
轴于点M,AB边交y轴于点H,连接BM.
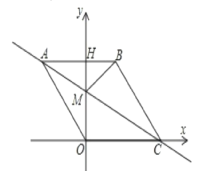
(1)菱形ABCO的边长是_________;
(2)求直线AC的解析式;
(3)动点P从点A出发,沿折线ABC的方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S,点P的运动时间为t秒,求S与t之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为奖励优秀学生,某校准备购买一批文具袋和圆规作为奖品,已知购买1个文具袋和2个圆规需21元,购买2个文具袋和3个圆规需39元。
(1)求文具袋和圆规的单价。
(2)学校准备购买文具袋20个,圆规若干,文具店给出两种优惠方案:
方案一:购买一个文具袋还送1个圆规。
方案二:购买圆规10个以上时,超出10个的部分按原价的八折优惠,文具袋不打折.
①设购买面规m个,则选择方案一的总费用为______,选择方案二的总费用为______.
②若学校购买圆规100个,则选择哪种方案更合算?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列推理证明.
已知:如图,AD∥EF,∠1=∠2.
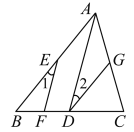
求证:AB∥DG.
证明:∵AD∥EF(________),
∴∠1=∠(_____)(________________)
∵∠1=∠2(已知),
∴∠________=∠2(________________________).
∴AB∥DG(______________________________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接2018年高中招生考试,某中学对全校九年级进行了一次数学摸底考试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成如下两幅不完整的统计图1和图2,请你根据图中所给的信息解答下列问题。
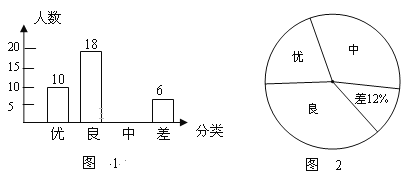
(1)请将表示成绩类别为“中”的条形统计图补充完整;
(2)在扇形统计图中表示成绩为“优”的扇形所对的圆心角为 度;
(3)学校九年级共有600人参加这次数学考试,估计该校有多少名学生成绩可以达到优.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填写下列证明过程中的推理根据:
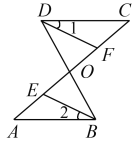
已知:如图所示,AC,BD相交于O,DF平分∠CDO与AC相交于F,BE平分于∠ABO与AC相交于E,∠A=∠C.求证:∠1=∠2.
证明:∵∠A=∠C(________),
∴AB∥CD (__________________________________),
∴∠ABO=∠CDO (__________________________________),
又∵∠1=![]() CDO,∠2=
CDO,∠2=![]() ∠ABO (__________________________________),
∠ABO (__________________________________),
∴∠1=∠2(____________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
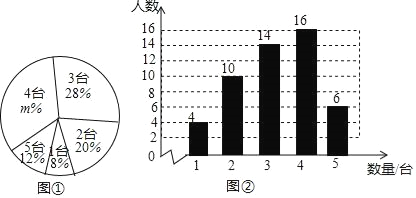
【题目】随着移动计算技术和无线网络的快速发展,移动学习方式越来越引起人们的关注,某校计划将这种学习方式应用到教育学中,从全校1500名学生中随机抽取了部分学生,对其家庭中拥有的移动设备的情况进行调查,并绘制出如下的统计图①和图②,根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为 ,图①中m的值为 ;
(2)求本次调查获取的样本数据的众数、中位数和平均数;
(3)根据样本数据,估计该校1500名学生家庭中拥有3台移动设备的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com