Question

【题目】已知四边形ABCD为菱形，其边长为6，，点P在菱形的边AD、CD及对角线AC上运动，当时，则DP的长为________.

Answer 1

【答案】2或或

【解析】

分以下三种情况求解：（1）点P在CD上，如图①，根据菱形的边长以及CP1=2DP1可得出结果；（2）点P在对角线AC上，如图②，在三角形CDP2中，可得出∠P2DC=90°，进而可得出DP2的长；（3）当点P在边AD上，如图③，过点D作于点F，过点作于点E，设，则，再用含x的代数式表示出CE，EP3，CP3的长，根据勾股定理列方程求解即可.

解：（1）当点P在CD上时，如解图①，

，，；

（2）当点P在对角线AC上时，如解图②，

，.

当时，，；

图① 图②

（3）当点P在边AD上时，如解图③，过点D作于点F，过点作于点E，设，则，

，，，，

，，

.

，在中，由勾股定理得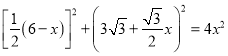，解得，（舍）.

综上所述，DP的长为2或或.

故答案为：2或或.