
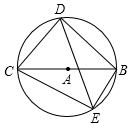
 如图,四边形BDCE内接于以BC为直径的⊙A,已知:BC=10,cos∠BCD=$\frac{3}{5}$,∠BCE=30°,则线段DE的长是3+4$\sqrt{3}$.
如图,四边形BDCE内接于以BC为直径的⊙A,已知:BC=10,cos∠BCD=$\frac{3}{5}$,∠BCE=30°,则线段DE的长是3+4$\sqrt{3}$. 分析 在Rt△CDB和Rt△CBE中,通过解直角三角形易求得BD、BE的长.
过B作BF⊥DE于F,由圆周角定理知∠BCE=∠BDE,∠BED=∠BCD.
根据这些角的三角函数值以及BD、BE的长,即可求得DF、EF的值,从而得到DE的长.
解答  解:过B作BF⊥DE于F.
解:过B作BF⊥DE于F.
在Rt△CBD中,BC=10,cos∠BCD=$\frac{3}{5}$,
∴BD=8.
在Rt△BCE中,BC=10,∠BCE=30°,
∴BE=5.
在Rt△BDF中,∠BDF=∠BCE=30°,BD=8,
∴DF=BD•cos30°=4$\sqrt{3}$.
在Rt△BEF中,∠BEF=∠BCD,即cos∠BEF=cos∠BCD=$\frac{3}{5}$,BE=5,
∴EF=BE•cos∠BEF=3.
∴DE=DF+EF=3+4$\sqrt{3}$,
故答案为:3+4$\sqrt{3}$.
点评 此题主要考查的是圆周角定理和解直角三角形的综合应用,难度适中.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知A、B、C三点共线,OC、OE分别平分∠AOD、∠DOB.
如图,已知A、B、C三点共线,OC、OE分别平分∠AOD、∠DOB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
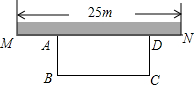 如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,
如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com