
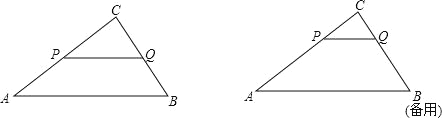
【题目】如图:已知△ABC中,AB=5,BC=3,AC=4,PQ∥AB,P点在AC上(与A、C不重合),Q在BC上.
(1)当△PQC的面积与四边形PABQ的面积相等时,求CP的长;
(2)当△PQC的周长与四边形PABQ的周长相等时,求CP的长;
(3)试问:在AB上是否存在一点M,使得△PQM为等腰直角三角形?若不存在,请简要说明理由;若存在,请求出PQ的长.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() 和
和![]() .
.
【解析】
(1)由于PQ∥AB,故△PQC∽△ABC,当△PQC的面积与四边形PABQ的面积相等时,△CPQ与△CAB的面积比为1:2,根据相似三角形的面积比等于相似比的平方,可求出CP的长;
(2)由于△PQC∽△ABC,根据相似三角形的性质,可用CP表示出PQ和CQ的长,进而可表示出AP、BQ的长.根据△CPQ和四边形ABQP的周长相等,可将相关的各边相加,即可求出CP的长;
(3)因为不能确定哪个角是直角,故应分类讨论.
①当∠MPQ=90°,且PM=PQ时.因为△CPQ∽△CAB,根据相似三角形边长的比等于高的比,可求出PQ的值;
②∠PQM=90°时与①相同;
③当∠PMQ=90°,且PM=MQ时,过M作ME⊥PQ,则ME=![]() PQ,根据相似三角形边长的比等于高的比,可求出PQ的值.
PQ,根据相似三角形边长的比等于高的比,可求出PQ的值.
(1)∵PQ∥AB,
∴△PQC∽△ABC,
∵S△PQC=S四边形PABQ,
∴S△PQC:S△ABC=1:2,
∴![]() ,
,
∴CP=![]() CA=2
CA=2![]() ;
;
(2)∵△PQC∽△ABC,
∴![]() ,
,
∴![]() ,
,
∴CQ=![]() CP,
CP,
同理:PQ=![]() CP,
CP,
∴l△PCQ=CP+PQ+CQ=CP+![]() CP+
CP+![]() CP=3CP,
CP=3CP,
I四边形PABQ=PA+AB+BQ+PQ,
=4﹣CP+AB+3﹣CQ+PQ,
=4﹣CP+5+3﹣![]() CP+
CP+![]() CP,
CP,
=12﹣![]() CP,
CP,
∴12﹣![]() CP=3CP,
CP=3CP,
∴![]() CP=12,
CP=12,
∴CP=![]() ;
;
(3)∵AC=4,AB=5,BC=3,
∴△ABC中AB边上的高为![]() ,
,
①当∠MPQ=90°,且PM=PQ时,

∵△CPQ∽△CAB,
∴![]() ,
,
∴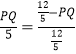 ,
,
∴PQ=![]() ;
;
②当∠PQM=90°时与①相同;
③当∠PMQ=90°,且PM=MQ时,
过M作ME⊥PQ,则ME=![]() PQ,
PQ,
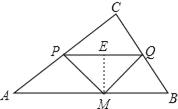
∴△CPQ的高为![]() ﹣ME=
﹣ME=![]() ﹣
﹣![]() PQ,
PQ,
∴![]() ,
,
∴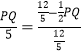 ,
,
∴PQ=![]() .
.
综合①②③可知:点M存在,PQ的长为![]() 或
或![]() .
.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD⊥AB,且CD2=ADDB,AE平分∠CAB交CD于F,∠EAB=∠B,CN=BE.①CF=BN;②∠ACB=90°;③FN∥AB;④AD2=DFDC.则下列结论正确的是( )
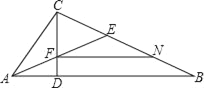
A. ①②④ B. ②③④ C. ①②③④ D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B为定点,定直线l//AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:
①线段MN的长;
②△PAB的周长;
③△PMN的面积;
④直线MN,AB之间的距离;
⑤∠APB的大小.
其中会随点P的移动而变化的是( )

A. ②③ B. ②⑤ C. ①③④ D. ④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:
①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF;⑤当△PMN∽△AMP时,点P是AB的中点.
其中正确的结论有
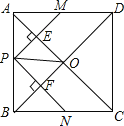
A.5个 B.4个 C.3个 D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
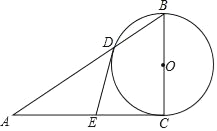
【题目】如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.
(1)求证:∠A=∠ADE;
(2)若AD=8,DE=5,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
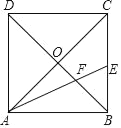
【题目】如图,正方形ABCD的边长为![]() +1,对角线AC、BD相交于点O,AE平分∠BAC分别交BC、BD于E、F,
+1,对角线AC、BD相交于点O,AE平分∠BAC分别交BC、BD于E、F,
(1)求证:△ABF∽△ACE;
(2)求tan∠BAE的值;
(3)在线段AC上找一点P,使得PE+PF最小,求出最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
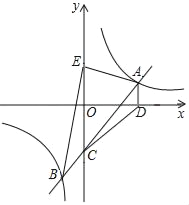
【题目】如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (m≠0)的图象交于点A、B,与y轴交于点C.过点A作AD⊥x轴于点D,AD=2,∠CAD=45°,连接CD,已知△ADC的面积等于6.
(m≠0)的图象交于点A、B,与y轴交于点C.过点A作AD⊥x轴于点D,AD=2,∠CAD=45°,连接CD,已知△ADC的面积等于6.
(1)求一次函数和反比例函数的解析式;
(2)若点E是点C关于x轴的对称点,求△ABE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com