

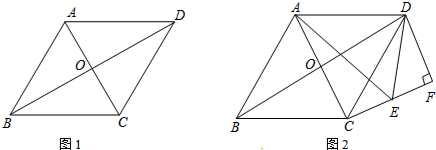
分析 (1)根据折叠得到AD=AC,所以△ADC是等腰三角形;
(2)设CE=x,利用勾股定理得到方程132-x2=152-(14-x)2解得:x=5,在Rt△AEC中,由勾股定理即可解答;
(3)猜想BC、BD、AE之间的数量关系为:BC-BD=2AE.由△ADC是等腰三角形,又∠DAC=90°,得到△ADC是等腰直角三角形又AE是CD边上的高,所以△AED与△AEC都是等腰直角三角形,即可得到CD=2AE.由BC-BD=CD,即可解答.
解答 解:(1)∵三角形ABC纸片,沿BC边上的高AE所在的直线翻折,使得点C与BC边上的点D重合.
∴AD=AC,
∴△ADC是等腰三角形;
故答案为:等腰.
(2)设CE=x,则BE=14-x,
在Rt△AEC中,由勾股定理得:AE2=AC2-CE2,
∴AE2=132-x2
在Rt△ABE中,由勾股定理得:AE2=AB2-BE2,
∴AE2=152-(14-x)2
∴132-x2=152-(14-x)2
解得:x=5,
在Rt△AEC中,由勾股定理得:$AE=\sqrt{A{C^2}-C{E^2}}=\sqrt{{{13}^2}-{5^2}}=\sqrt{144}=12$.
(3)猜想BC、BD、AE之间的数量关系为:BC-BD=2AE.
证明如下:
由(1)得:△ADC是等腰三角形,又∠DAC=90°,
∴△ADC是等腰直角三角形
又AE是CD边上的高,
∴DE=CE,$∠DAE=∠EAC=\frac{1}{2}∠DAC=\frac{1}{2}×90°=45°$,
∴△AED与△AEC都是等腰直角三角形,
∴DE=AE=EC,即CD=2AE.
∵BC-BD=CD
∴BC-BD=2AE.
点评 本题考查了等腰三角形的性质定理与判定定理、等腰直角三角形的性质、勾股定理,解决本题的根据是判定△ADC是等腰三角形和勾股定理的应用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 劳动时间(小时) | 3 | 4 | 5 | 6 |
| 人数 | 1 | 1 | 2 | 1 |
| A. | 中位数是5,平均数是3.6 | B. | 众数是5,平均数是4.6 | ||
| C. | 中位数是4,平均数是3.6 | D. | 众数是2,平均数是4.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
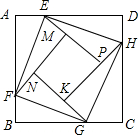 如图正方形ABCD的边长为2,点E、F、G、H分别在AD、AB、BC、CD上的点,且AE=BF=CG=DH,分别将△AEF、△BFG、△CGH、△DHE沿EF、FG、GH、HE翻折,得四边形MNKP,设AE=x,S四边形MNKP=y,则y关于x的函数图象大致为( )
如图正方形ABCD的边长为2,点E、F、G、H分别在AD、AB、BC、CD上的点,且AE=BF=CG=DH,分别将△AEF、△BFG、△CGH、△DHE沿EF、FG、GH、HE翻折,得四边形MNKP,设AE=x,S四边形MNKP=y,则y关于x的函数图象大致为( )| A. | 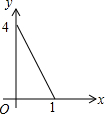 | B. | 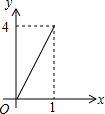 | C. | 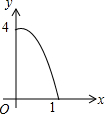 | D. | 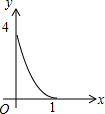 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
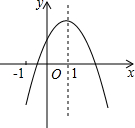 二次函数y=ax2+bx+c的图象如图所示,且P=|2a+b|+|3b-2c|,Q=|2a-b|-|3b+2c|,则P,Q的大小关系是P>Q.
二次函数y=ax2+bx+c的图象如图所示,且P=|2a+b|+|3b-2c|,Q=|2a-b|-|3b+2c|,则P,Q的大小关系是P>Q.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com