
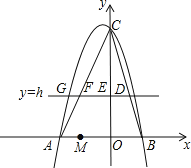
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Å×ĪļĻßy£½ax2+bx+6¾¹żµćA£Ø©3£¬0£©ŗĶµćB£Ø2£¬0£©£¬Ö±Ļßy£½h£ØhĪŖ³£Źż£¬ĒŅ0£¼h£¼6£©ÓėBC½»ÓŚµćD£¬ÓėyÖį½»ÓŚµćE£¬ÓėAC½»ÓŚµćF£®
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©Į¬½ÓAE£¬ĒóhĪŖŗĪÖµŹ±£¬”÷AEFµÄĆ껿×ī“ó£®
£Ø3£©ŅŃÖŖŅ»¶ØµćM£Ø©2£¬0£©£¬ĪŹ£ŗŹĒ·ń“ęŌŚÕāŃłµÄÖ±Ļßy£½h£¬Ź¹”÷BDMŹĒµČŃüČż½ĒŠĪ£æČō“ęŌŚ£¬ĒėĒó³öhµÄÖµŗĶµćDµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©y£½©x2©x+6£»£Ø2£©µ±h£½3Ź±£¬”÷AEFµÄĆ껿×ī“ó£¬×ī“óĆ껿ŹĒ ![]() £®£Ø3£©“ęŌŚ£¬µ±h£½
£®£Ø3£©“ęŌŚ£¬µ±h£½![]() Ź±£¬µćDµÄ×ų±źĪŖ£Ø
Ź±£¬µćDµÄ×ų±źĪŖ£Ø![]() £¬
£¬![]() £©£»µ±h£½
£©£»µ±h£½![]() Ź±£¬µćDµÄ×ų±źĪŖ£Ø
Ź±£¬µćDµÄ×ų±źĪŖ£Ø![]() £¬
£¬![]() £©£®
£©£®
”¾½āĪö”æ
£Ø1£©ĄūÓĆ“ż¶ØĻµŹż·Ø¼“æɽā¾öĪŹĢā£®
£Ø2£©ÓÉĢāŅāæɵƵćEµÄ×ų±źĪŖ£Ø0£¬h£©£¬µćFµÄ×ų±źĪŖ£Ø ![]() £¬h£©£¬øł¾ŻS”÷AEF£½
£¬h£©£¬øł¾ŻS”÷AEF£½![]() OEFE£½
OEFE£½![]() h
h![]() £½©
£½©![]() £Øh©3£©2+
£Øh©3£©2+![]() £®ĄūÓƶž“ĪŗÆŹżµÄŠŌÖŹ¼“æɽā¾öĪŹĢā£®
£®ĄūÓƶž“ĪŗÆŹżµÄŠŌÖŹ¼“æɽā¾öĪŹĢā£®
£Ø3£©“ęŌŚ£®·ÖĮ½ÖÖĒéŠĪĒéŠĪ£¬·Ö±šĮŠ³ö·½³Ģ¼“æɽā¾öĪŹĢā£®
½ā£ŗČēĶ¼£ŗ
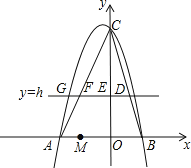
£Ø1£©”ßÅ×ĪļĻßy£½ax2+bx+6¾¹żµćA£Ø©3£¬0£©ŗĶµćB£Ø2£¬0£©£¬
”ą![]() £¬
£¬
½āµĆ£ŗ![]() £®
£®
”ąÅ×ĪļĻߵĽāĪöŹ½ĪŖy£½©x2©x+6£®
£Ø2£©”ß°Ńx£½0“śČėy£½©x2©x+6£¬µĆy£½6£¬
”ąµćCµÄ×ų±źĪŖ£Ø0£¬6£©£¬
Éč¾¹żµćAŗĶµćCµÄÖ±ĻߵĽāĪöŹ½ĪŖy£½mx+n£¬Ōņ![]() £¬
£¬
½āµĆ ![]() £¬
£¬
”ą¾¹żµćAŗĶµćCµÄÖ±ĻߵĽāĪöŹ½ĪŖ£ŗy£½2x+6£¬
”ßµćEŌŚÖ±Ļßy£½hÉĻ£¬
”ąµćEµÄ×ų±źĪŖ£Ø0£¬h£©£¬
”ąOE£½h£¬
”ßµćFŌŚÖ±Ļßy£½hÉĻ£¬
”ąµćFµÄׯ×ų±źĪŖh£¬
°Ńy£½h“śČėy£½2x+6£¬µĆh£½2x+6£¬
½āµĆx£½![]() £¬
£¬
”ąµćFµÄ×ų±źĪŖ£Ø ![]() £¬h£©£¬
£¬h£©£¬
”ąEF£½![]() £®
£®
”ąS”÷AEF£½![]() OEFE£½
OEFE£½![]() h
h![]() £½©
£½©![]() £Øh©3£©2+
£Øh©3£©2+![]() £¬
£¬
”ß©![]() £¼0ĒŅ0£¼h£¼6£¬
£¼0ĒŅ0£¼h£¼6£¬
”ąµ±h£½3Ź±£¬”÷AEFµÄĆ껿×ī“ó£¬×ī“óĆ껿ŹĒ![]() £®
£®
£Ø3£©“ęŌŚ·ūŗĻĢāŅāµÄÖ±Ļßy£½h£®
”ßB£Ø2£¬0£©£¬C£Ø0£¬6£©£¬
”ąÖ±ĻßBCµÄ½āĪöŹ½ĪŖy£½©3x+6£¬ÉčD£Øm£¬©3m+6£©£®
¢Łµ±BM£½BDŹ±£¬£Øm©2£©2+£Ø©3m+6£©2£½42£¬
½āµĆm£½![]() »ņ
»ņ![]() £ØÉįĘś£©£¬
£ØÉįĘś£©£¬
”ąD£Ø![]() £¬
£¬![]() £©£¬“ĖŹ±h£½
£©£¬“ĖŹ±h£½![]() £®
£®
¢Śµ±MD£½BMŹ±£¬£Øm+2£©2+£Ø©3m+6£©2£½42£¬
½āµĆm£½![]() »ņ2£ØÉįĘś£©£¬
»ņ2£ØÉįĘś£©£¬
”ąD£Ø![]() £¬
£¬![]() £©£¬“ĖŹ±h£½
£©£¬“ĖŹ±h£½![]() £®
£®
”ß×ŪÉĻĖłŹö£¬“ęŌŚÕāŃłµÄÖ±Ļßy£½![]() »ņy£½
»ņy£½![]() £¬Ź¹”÷BDMŹĒµČŃüČż½ĒŠĪ£¬µ±h£½
£¬Ź¹”÷BDMŹĒµČŃüČż½ĒŠĪ£¬µ±h£½![]() Ź±£¬µćDµÄ×ų±źĪŖ£Ø
Ź±£¬µćDµÄ×ų±źĪŖ£Ø![]() £¬
£¬![]() £©£»µ±h£½
£©£»µ±h£½![]() Ź±£¬µćDµÄ×ų±źĪŖ£Ø
Ź±£¬µćDµÄ×ų±źĪŖ£Ø![]() £¬
£¬![]() £©£®
£©£®


 ĆūŠ£æĪĢĆĻµĮŠ“š°ø
ĆūŠ£æĪĢĆĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŠ£¾ÅÄź¼¶Ń§ÉśÄ³æĘÄæѧʌ×ÜĘĄ³É¼ØŹĒÓÉĶź³É×÷Ņµ”¢µ„ŌŖ¼ģ²ā”¢ĘŚÄ©æ¼ŹŌČżĻī³É¼Ø¹¹³ÉµÄ£¬Čē¹ūѧʌ×ÜĘĄ³É¼Ø80·ÖŅŌÉĻ£Øŗ¬80·Ö£©£¬ŌņĘĄ¶ØĪŖ”°ÓÅŠć”±£¬ĻĀ±ķŹĒŠ”ÕÅŗĶŠ”ĶõĮ½Ī»Ķ¬Ń§µÄ³É¼Ø¼ĒĀ¼£ŗ
Ķź³É×÷Ņµ | µ„ŌŖ²āŹŌ | ĘŚÄ©æ¼ŹŌ | |
Š”ÕÅ | 70 | 90 | 80 |
Š”Ķõ | 60 | 75 | _______ |
Čō°“Ķź³É×÷Ņµ”¢µ„ŌŖ¼ģ²ā”¢ĘŚÄ©æ¼ŹŌČżĻī³É¼Ø°“1£ŗ2£ŗ7µÄČØÖŲĄ“Č·¶Øѧʌ×ÜĘĄ³É¼Ø£®
£Ø1£©Ēė¼ĘĖ抔ÕŵÄѧʌ×ÜĘĄ³É¼ØĪŖ¶ąÉŁ·Ö£æ
£Ø2£©Š”ĶõŌŚĘŚÄ©£ØĘŚÄ©³É¼ØĪŖÕūŹż£©Ó¦øĆ×īÉŁæ¼¶ąÉŁ·Ö²ÅÄÜ“ļµ½ÓÅŠć£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŹÖ»śĻĀŌŲŅ»øöAPP£¬½ÉÄÉŅ»¶ØŹż¶īµÄŃŗ½š£¬¾ĶÄÜŅŌĆ抔Ź±0.5µ½1ŌŖµÄ¼Ūøń½āĖųŅ»Į¾×ŌŠŠ³µČĪŅāĘļŠŠ”×ī½üµÄĶųŗģ·Ē”°¹²Ļķµ„³µ”±ÄŖŹō£®¹²Ļķµ„³µĪŖ½ā¾öŹŠĆń³öŠŠµÄ”°×īŗóŅ»¹«Ąļ”±ÄŃĢā°ļĮĖ“óƦ£¬ČĖĆĒŌŚĻķŹÜæĘ¼¼½ų²½”¢¹²Ļķ¾¼Ć“ųĄ“µÄ±ćĄūµÄĶ¬Ź±£¬ĖęŅāĶ£·Å”¢¼Ó×°Ė½Ėų”¢“󊶰ĖæéµČ»Ł»µµ„³µµÄŠŠĪŖŅ²²ć³ö²»Ēī£®Ä³¹²Ļķµ„³µ¹«Ė¾Ņ»ŌĀĶ¶Čė²æ·Ö×ŌŠŠ³µ½ųČėŹŠ³”£¬Ņ»ŌĀµ×·¢ĻÖĖš»µĀŹ²»µĶÓŚ10%£¬¶žŌĀ³õÓÖĶ¶Čė1200Į¾½ųČėŹŠ³”£¬Ź¹æÉŹ¹ÓƵÄ×ŌŠŠ³µ“ļµ½7500Į¾£®
£Ø1£©Ņ»ŌĀ·ŻøĆ¹«Ė¾Ķ¶ČėŹŠ³”µÄ×ŌŠŠ³µÖĮÉŁÓŠ¶ąÉŁĮ¾£æ
£Ø2£©¶žŌĀ·ŻµÄĖš»µĀŹ“ļµ½20%£¬½ųČėČżŌĀ·Ż£¬øĆ¹«Ė¾ŠĀĶ¶ČėŹŠ³”µÄ×ŌŠŠ³µ±Č¶žŌĀ·ŻŌö³¤4a%£¬ÓÉÓŚĆ½ĢåµÄ¹Ų×¢£¬»Ł»µ¹²Ļķµ„³µµÄŠŠĪŖŅżĘšĮĖŅ»³”¹śĆńĖŲÖŹµÄ“óĢÖĀŪ£¬ČżŌĀ·ŻµÄĖš»µĀŹĻĀ½µ![]() a%£¬ČżŌĀµ×æÉŹ¹ÓƵÄ×ŌŠŠ³µ“ļµ½7752Į¾£¬ĒóaµÄÖµ£®
a%£¬ČżŌĀµ×æÉŹ¹ÓƵÄ×ŌŠŠ³µ“ļµ½7752Į¾£¬ĒóaµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
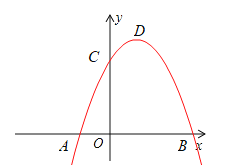
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ¶ž“ĪŗÆŹż![]() µÄĶ¼ĻóÓė
µÄĶ¼ĻóÓė![]() Öį½»ÓŚ
Öį½»ÓŚ![]() Į½µć£Øµć
Į½µć£Øµć![]() ŌŚµć
ŌŚµć![]() µÄ×ó²ą£©£¬Óė
µÄ×ó²ą£©£¬Óė![]() Öį½»ÓŚµć
Öį½»ÓŚµć![]() £¬¶„µćĪŖµć
£¬¶„µćĪŖµć![]() .
.
£Ø1£©µć![]() µÄ×ų±źĪŖ £¬µć
µÄ×ų±źĪŖ £¬µć![]() µÄ×ų±źĪŖ £»£ØÓĆŗ¬ÓŠ
µÄ×ų±źĪŖ £»£ØÓĆŗ¬ÓŠ![]() µÄ“śŹżŹ½±ķŹ¾£©
µÄ“śŹżŹ½±ķŹ¾£©
£Ø2£©Į¬½Ó![]() .
.
¢ŁČō![]() Ę½·Ö
Ę½·Ö![]() £¬Ē󶞓ĪŗÆŹżµÄ±ķ“ļŹ½£»
£¬Ē󶞓ĪŗÆŹżµÄ±ķ“ļŹ½£»
¢ŚĮ¬½Ó![]() £¬Čō
£¬Čō![]() Ę½·Ö
Ę½·Ö![]() £¬Ē󶞓ĪŗÆŹżµÄ±ķ“ļŹ½.
£¬Ē󶞓ĪŗÆŹżµÄ±ķ“ļŹ½.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ[ĪŹĢāĢį³ö]
ŌŚÅŠ¶ØĮ½øöČż½ĒŠĪČ«µČŹ±£¬³żøł¾ŻŅ»°ćČż½ĒŠĪČ«µČÅŠ¶Ø¶ØĄķĶā£¬»¹ÓŠ"![]() " ·½·Ø.ĄąĖʵÄ,ĪŅĆĒ¶ŌÖ±½ĒČż½ĒŠĪĻąĖʵÄĢõ¼ž½ųŠŠĢ½Ė÷”£
" ·½·Ø.ĄąĖʵÄ,ĪŅĆĒ¶ŌÖ±½ĒČż½ĒŠĪĻąĖʵÄĢõ¼ž½ųŠŠĢ½Ė÷”£
(1) [Ģį³ö²ĀĻė]
³żøł¾ŻŅ»°ćČż½ĒŠĪĻąĖĘÅŠ¶ØµÄĢõ¼žĶā£¬ĒėÄćĢį³öĄąĖĘÓŚ"![]() "µÄÅŠ¶ØÖ±½ĒČż½ĒŠĪĻąĖʵķ½·Ø£¬²¢ÓĆĪÄ×ÖĆčŹöĪŖ: .
"µÄÅŠ¶ØÖ±½ĒČż½ĒŠĪĻąĖʵķ½·Ø£¬²¢ÓĆĪÄ×ÖĆčŹöĪŖ: .
(2) [³õ²½Ė¼æ¼]
ĘäÖŠ£¬ĪŅĆĒ²»·Į½«ĪŹĢāÓĆ·ūŗÅÓļŃŌ±ķŹ¾ĪŖ:ČēĶ¼1,ŌŚ![]() ŗĶ
ŗĶ![]() ÖŠ£¬
ÖŠ£¬![]() ,Čō ,Ōņ
,Čō ,Ōņ![]() £¬ ĒėøųÓčÖ¤Ć÷.
£¬ ĒėøųÓčÖ¤Ć÷.


(3) [ÉīČėŃŠ¾æ]
ČōĶ¼2ÖŠµÄ![]() ,ĘäĖūĢõ¼ž²»±ä£¬Į½øöČż½ĒŠĪŹĒ·ńĻąĖĘ?ŹŌĄūÓĆŅŌÉĻĢ½¾æµÄ½įĀŪ½ā¾öĪŹĢā,ČōĻąĖĘĒėÖ¤Ć÷,Čō²»ĻąĖĘ£¬Ēė»³ö·“Ąż.
,ĘäĖūĢõ¼ž²»±ä£¬Į½øöČż½ĒŠĪŹĒ·ńĻąĖĘ?ŹŌĄūÓĆŅŌÉĻĢ½¾æµÄ½įĀŪ½ā¾öĪŹĢā,ČōĻąĖĘĒėÖ¤Ć÷,Čō²»ĻąĖĘ£¬Ēė»³ö·“Ąż.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
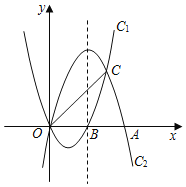
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻßC1£ŗy£½x2©2xÓėÅ×ĪļĻßC2£ŗy£½ax2+bxæŖæŚ“óŠ”ĻąĶ¬”¢·½ĻņĻą·“£¬ĖüĆĒĻą½»ÓŚO£¬CĮ½µć£¬ĒŅ·Ö±šÓėxÖįµÄÕż°ėÖį½»ÓŚµćB£¬µćA£¬OA£½2OB£®
£Ø1£©ĒóÅ×ĪļĻßC2µÄ½āĪöŹ½£»
£Ø2£©ŌŚÅ×ĪļĻßC2µÄ¶Ō³ĘÖįÉĻŹĒ·ń“ęŌŚµćP£¬Ź¹PA+PCµÄÖµ×īŠ”£æČō“ęŌŚ£¬Ēó³öµćPµÄ×ų±ź£¬Čō²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£»
£Ø3£©MŹĒÖ±ĻßOCÉĻ·½Å×ĪļĻßC2ÉĻµÄŅ»øö¶Æµć£¬Į¬½ÓMO£¬MC£¬MŌĖ¶Æµ½Ź²Ć“Ī»ÖĆŹ±£¬”÷MOCĆ껿×ī“ó£æ²¢Ēó³ö×ī“óĆ껿£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ°ĖÄź¼¶£Ø1£©°ąŃŠ¾æŠŌѧĻ°Š”×éĪŖŃŠ¾æČ«Š£Ķ¬Ń§æĪĶāŌĶĮĒéæö£¬ŌŚČ«Š£Ė껜ŃūĒėĮĖ²æ·ÖĶ¬Ń§²ĪÓėĪŹ¾ķµ÷²é£¬Ķ³¼ĘĶ¬Ń§ĆĒŅ»øöŌĀŌĶĮæĪĶāŹéµÄŹżĮ棬²¢»ęÖĘĮĖŅŌĻĀĶ³¼ĘĶ¼£®

Ēėøł¾ŻĶ¼ÖŠŠÅĻ¢½ā¾öĻĀĮŠĪŹĢā£ŗ
£Ø1£©¹²ÓŠ¶ąÉŁĆūĶ¬Ń§²ĪÓėĪŹ¾ķµ÷²é£»
£Ø2£©²¹Č«ĢõŠĪĶ³¼ĘĶ¼ŗĶÉČŠĪĶ³¼ĘĶ¼£»
£Ø3£©Č«Š£¹²ÓŠŃ§Éś1500ČĖ£¬Ēė¹Ą¼ĘøĆŠ£Ń§ÉśŅ»øöŌĀŌĶĮ2±¾æĪĶāŹéµÄČĖŹżŌ¼ĪŖ¶ąÉŁ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬¹żµćM£Ø0£¬2£©µÄÖ±ĻßlÓėxÖįĘ½ŠŠ£¬ĒŅÖ±Ļßl·Ö±šÓė·“±ČĄżŗÆŹży£½![]() £Øx£¾0£©ŗĶy£½
£Øx£¾0£©ŗĶy£½![]() £Øx£¼0£©µÄĶ¼Ļó·Ö±š½»ÓŚµćP£¬Q£®
£Øx£¼0£©µÄĶ¼Ļó·Ö±š½»ÓŚµćP£¬Q£®
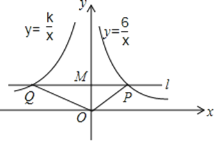
£Ø1£©ĒóPµćµÄ×ų±ź£»
£Ø2£©Čō”÷POQµÄĆ껿ĪŖ9£¬ĒókµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚµŲĆęÉĻŹśÖ±°²×°×ÅAB”¢CD”¢EFČżøłĮ¢Öł£¬ŌŚĶ¬Ņ»Ź±æĢĶ¬Ņ»¹āŌ“ĻĀĮ¢ÖłAB”¢CDŠĪ³ÉµÄÓ°×ÓĪŖBGÓėDH.

£Ø1£©ĢīæÕ£ŗÅŠ¶Ļ“Ė¹āŌ“ĻĀŠĪ³ÉµÄĶ¶Ó°ŹĒ£ŗ Ķ¶Ó°.
£Ø2£©×÷³öĮ¢ÖłEFŌŚ“Ė¹āŌ“ĻĀĖłŠĪ³ÉµÄÓ°×Ó.
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com