
【题目】已知![]() 、
、![]() 两地之间有一条270千米的公路,甲、乙两车同时出发,甲车以每小时60千米/时的速度沿此公路从
两地之间有一条270千米的公路,甲、乙两车同时出发,甲车以每小时60千米/时的速度沿此公路从![]() 地匀速开往
地匀速开往![]() 地,乙车从
地,乙车从![]() 地沿此公路匀速开往
地沿此公路匀速开往![]() 地,两车分别到达目的地后停止甲、乙两车相距的路程
地,两车分别到达目的地后停止甲、乙两车相距的路程![]() (千米)与甲车的行驶时间
(千米)与甲车的行驶时间![]() (时)之间的函数关系如图所示:
(时)之间的函数关系如图所示:
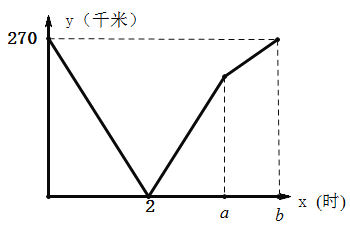
(1)乙年的速度为______千米/时,![]() _____,
_____,![]() ______.
______.
(2)求甲、乙两车相遇后![]() 与
与![]() 之间的函数关系式,并写出相应的自变量
之间的函数关系式,并写出相应的自变量![]() 的取值范围.
的取值范围.
【答案】(1)75;3.6;4.5;(2) 当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
【解析】
(1)根据图像可知两车2小时候相遇,根据路程和为270千米即可求出乙车的速度,然后根据“路程、速度、时间”的关系确定![]() 、b的值;
、b的值;
(2)根据图像可知相遇后图像分为两段,将相遇后点的坐标和分段处以及到达B地后的坐标分别表示出来,然后运用待定系数法解决即可;
解:(1)乙车的速度为:(270-60×2)÷2=75(千米/时);
![]() =270÷75=3.6,b=270÷60=4.5
=270÷75=3.6,b=270÷60=4.5
故答案为:75;3.6;4.5;
(2)60×3.6=216(千米),如图,可得![]() ,
,![]() ,
,![]() .
.
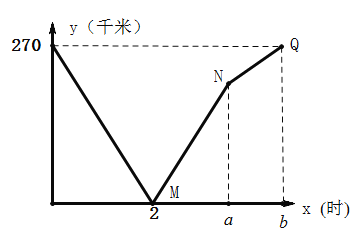
设当![]() 时的解析式为
时的解析式为![]() ,
,
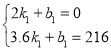 ,
,
解得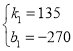
![]() 当
当![]() 时,
时,![]() ,
,
设当![]() 时的解析式为
时的解析式为![]() ,则
,则
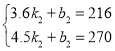 ,
,
解得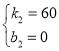 ,
,
当![]() 时,
时,![]() .
.


科目:初中数学 来源: 题型:
【题目】如图线段AB的端点在边长为1的正方形网格的格点上,现将线段AB绕点A按逆时针方向旋转90°得到线段AC.
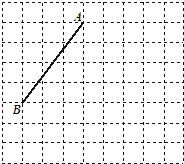
(1)请你用尺规在所给的网格中画出线段AC及点B经过的路径;
(2)若将此网格放在一平面直角坐标系中,已知点A的坐标为(1,3),点B的坐标为(-2,-1),则点C的坐标为 ;
(3)线段AB在旋转到线段AC的过程中,线段AB扫过的区域的面积为 ;
(4)若有一张与(3)中所说的区域形状相同的纸片,将它围成一个几何体的侧面,则该几何体底面圆的半径长为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的部分图象如图,顶点是
的部分图象如图,顶点是![]() .
.
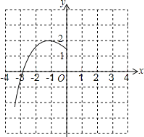
(1)求二次函数的解析式;
(2)若抛物线上两点![]() 、
、![]() 的横坐标满足
的横坐标满足![]() ,则
,则![]() ________
________![]() ;(用“
;(用“![]() ”、“
”、“![]() ”或“
”或“![]() ”填空)
”填空)
(3)观察图象,直接写出当![]() 时,
时,![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,过点F(0,1)的直线y=kx+b与抛物线![]() 交于M(x1,y1)和N(x2,y2)两点(其中x1<0,x2<0).
交于M(x1,y1)和N(x2,y2)两点(其中x1<0,x2<0).
⑴求b的值.
⑵求x1x2的值
⑶分别过M、N作直线l:y=-1的垂线,垂足分别是M1、N1,判断△M1FN1的形状,并证明你的结论.
⑷对于过点F的任意直线MN,是否存在一条定直线m,使m与以MN为直径的圆相切.如果有,请法度出这条直线m的解析式;如果没有,请说明理由.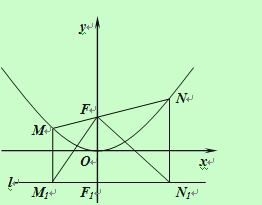
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】机器人“海宝”在某圆形区域表演“按指令行走”,如图所示,“海宝”从圆心O出发,先沿北偏西67.4°方向行走13米至点A处,再沿正南方向行走14米至点B处,最后沿正东方向行走至点C处,点B、C都在圆O上.
(1)求弦BC的长;
(2)求圆O的半径长.
(本题参考数据:sin 67.4° =![]() ,cos 67.4°=
,cos 67.4°=![]() ,tan 67.4° =
,tan 67.4° =![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是圆
是圆![]() 的直径,
的直径,![]() ,点
,点![]() 是圆
是圆![]() 上一动点(与
上一动点(与![]() ,
,![]() 不重合),
不重合),![]() 的平分线交圆
的平分线交圆![]() 于
于![]() .
.
![]() 判断
判断![]() 的形状,并证明你的结论;
的形状,并证明你的结论;
![]() 若
若![]() 是
是![]() 的内心,当点
的内心,当点![]() 运动时,
运动时,![]() 、
、![]() 中是否存在长度保持不变的线段?如果存在,请指出并求其长度;如果不存在,请说明理由.
中是否存在长度保持不变的线段?如果存在,请指出并求其长度;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点
轴分别相交于点![]() 、点
、点![]() ,
,![]() ,若将
,若将![]() 沿直线
沿直线![]() 折叠,使点
折叠,使点![]() 与点
与点![]() 重合,折痕
重合,折痕![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 交于点
交于点![]() .
.
(1)求![]() 的值;
的值;
(2)求点![]() 的坐标;
的坐标;
(3)求直线![]() 的表达式.
的表达式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com