
【题目】在平行四边形![]() 中,对角线
中,对角线![]() 交于点
交于点![]() ,
,![]() 点
点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;同时,点
;同时,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;当一个点停止运动时,另一个点也停止运动.连接
;当一个点停止运动时,另一个点也停止运动.连接![]() ,过点
,过点![]() 作
作![]() ,设运动时间为
,设运动时间为![]() ,解答下列问题:
,解答下列问题:
(1)当![]() 为何值时
为何值时![]() ;
;
(2)在运动过程中,是否存在某一时刻![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)当![]() 为何值时
为何值时![]() 是等腰三角形?
是等腰三角形?
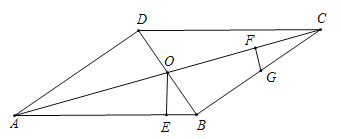
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() 或
或![]()
【解析】
(1)由已知易得![]() ,要求
,要求![]() ,只要
,只要![]() 即可.根据相似三角形性质列式计算即可.
即可.根据相似三角形性质列式计算即可.
(2)由图可知![]() ,根据平行四边形面积可求
,根据平行四边形面积可求![]() ,
,![]() ,进而用t表示出
,进而用t表示出![]() 的面积;再由
的面积;再由![]() ,由相似三角形的面积比可求得
,由相似三角形的面积比可求得![]() 的面积,从而根据
的面积,从而根据![]() 列方程即可解答;
列方程即可解答;
(3)分三种情况讨论,当![]() 、
、![]() 、
、![]() 时,分别根据等腰三角形三线合一性质和相似三角形性质,由比例式列方程求解即可.
时,分别根据等腰三角形三线合一性质和相似三角形性质,由比例式列方程求解即可.
解:(1)∵![]()
∴![]()
∴![]()
∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
当![]() 时,
时,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]()
∴![]() ;
;
(2)由(1)可知![]() ,
,
∴![]() ,
,![]()
∴![]() ,
,
又∵![]()
∴![]() ,
,
∴![]() ,
,
∴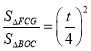 ,
,
∴![]() ,
,
∴![]() ,
,
当![]() 时,即
时,即![]() ,
,
即![]()
解得:![]() ,
,![]() (舍)
(舍)
所以当![]() 时,
时,![]() ;
;
(3)①当![]() 时,
时,
![]() ;
;
②当![]() 时,过O点作OG⊥AB,如图:
时,过O点作OG⊥AB,如图:
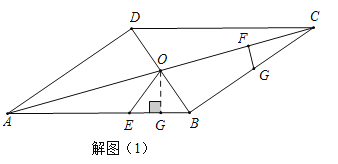
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
即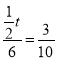 ,
,
解得:![]() ;
;
③当![]() 时,
时,
过![]() 作
作![]() 于
于![]() ,
,

则![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
即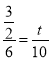 ,
,
∴![]() ,
,
所以当![]() 或
或![]() 或
或![]() 时,
时,![]() 是等腰三角形.
是等腰三角形.


科目:初中数学 来源: 题型:
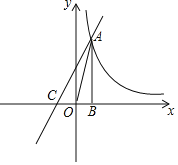
【题目】如图,已知反比例函数y=![]() 的图象经过第一象限内的一点A(n,4),过点A作AB⊥x轴于点B,且△AOB的面积为2.
的图象经过第一象限内的一点A(n,4),过点A作AB⊥x轴于点B,且△AOB的面积为2.
(1)求m和n的值;
(2)若一次函数y=kx+2的图象经过点A,并且与x轴相交于点C,求线段AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
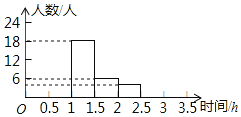
【题目】为减轻学生的作业负担,某地教育局规定初中阶段学生每晚的作业量不超过1.5小时,一个月后,九年一班芳芳对本班每位同学晚上作业时间进行了一次调查,并根据收集的数据绘制了如图所示的不完整的频数分布直方图(每组包含最大值,不包含最小值),并知1﹣1.5h占45%,2~2.5h占10%,请根据以上信息解答问题.
(1)求该班共有多少名学生;
(2)求该班作业时间不超过1小时和超过2.5小时的共有多少人;
(3)若该市九年级共有3000名学生,请估计他们中完成作业超过1.5小时而不超过2.5小时的有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】碑林书法社小组用的书法练习纸(毛边纸可以到甲商店购买,也可以到乙商店购买已知两商店的标价都是每刀20元(每刀100张),但甲商店的优惠条件是:若购买不超过10刀,则按标价买,购买10以上,从第11刀开始按标价的七折卖;乙商店的优惠条件是:购买一只9元的毛笔,从第一刀开始按标价的八五折卖.购买刀数为![]() (刀),在甲商店购买所需费用为
(刀),在甲商店购买所需费用为![]() 元,在乙商店购买所需费用为
元,在乙商店购买所需费用为![]() 元.
元.
(1)写出![]() 、
、![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(2)求在乙商店购买所需总费用小于甲商店购买所需总费用时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
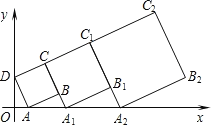
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第1个正方形A1B1C1C;延长C1B1交x轴于点A2,作第2个正方形A2B2C2C1,…,按这样的规律进行下去,第2019个正方形的面积是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了增强学生的环保意识,某校组织了一次全校2000名学生都参加的“环保知识”考试,考题共10题.考试结束后,学校团委随机抽查部分考生的考卷,对考生答题情况进行分析统计,发现所抽查的考卷中答对题量最少为6题,并且绘制了如下两幅不完整的统计图.请根据统计图提供的信息解答以下问题: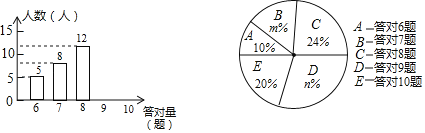
(1)本次抽查的样本容量是 ;在扇形统计图中,m= ,n= ,“答对8题”所对应扇形的圆心角为 度;
(2)将条形统计图补充完整;
(3)请根据以上调查结果,估算出该校答对不少于8题的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长均为1的方格纸中,线段AB的端点A、B均在小正方形的顶点上.
(1)在方格纸中画出以AB为一条直角边的等腰直角△ABC,顶点C在小正方形的顶点上;
(2)在方格纸中画出△ABC的中线BD,将线段DC绕点C顺时针旋转90°得到线段CD′,画出旋转后的线段CD′,连接BD′,直接写出四边形BDCD′的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校调查了若干名家长对“初中生带手机上学”现象的看法,统计整理并制作了如下的条形与扇形统计图,根据图中提供的信息,完成以下问题:
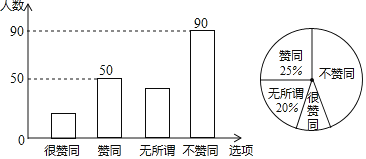
(1)本次共调查了 名家长;扇形统计图中“很赞同”所对应的圆心角是 度.已知该校共有1600名家长,则“不赞同”的家长约有 名;请补全条形统计图;
(2)从“不赞同”的五位家长中(两女三男),随机选取两位家长对全校家长进行“学生使用手机危害性”的专题讲座,请用树状图或列表法求出选中“1男1女”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com