
【题目】在坐标系xOy中,抛物线y=﹣x2+bx+c经过点A(﹣3,0)和B(1,0),与y轴交于点C,
(1)求抛物线的表达式;
(2)若点D为此抛物线上位于直线AC上方的一个动点,当△DAC的面积最大时,求点D的坐标;
(3)设抛物线顶点关于y轴的对称点为M,记抛物线在第二象限之间的部分为图象G.点N是抛物线对称轴上一动点,如果直线MN与图象G有公共点,请结合函数的图象,直接写出点N纵坐标t的取值范围.
【答案】(1)y=﹣x2﹣2x+3;(2)D(﹣![]() ,
, ![]() );(3)当2<t≤4时,直线MN与函数图象G有公共点.
);(3)当2<t≤4时,直线MN与函数图象G有公共点.
【解析】试题分析:(1)设抛物线的解析式为y=a(x+3)(x﹣1),然后将a=﹣1代入即可求得抛物线的解析式;
(2)过点D作DE∥y轴,交AC于点E.先求得点C的坐标,然后利用待定系数法求得直线AC的解析式,设点D的坐标为![]() ,则E点的坐标为(x,x+3),于是得到DE的长(用含x的式子表示,接下来,可得到△ADC的面积与x的函数关系式,最后依据配方法可求得三角形的面积最大时,点D的坐标;
,则E点的坐标为(x,x+3),于是得到DE的长(用含x的式子表示,接下来,可得到△ADC的面积与x的函数关系式,最后依据配方法可求得三角形的面积最大时,点D的坐标;
(3)如图2所示:先求得抛物线的顶点坐标,于是可得到点M的坐标,可判断出点M在直线AC上,从而可求得点N的坐标,当点N′与抛物线的顶点重合时,N′的坐标为(﹣1,4),于是可确定出t的取值范围.
试题解析:(1)设抛物线的解析式为y=a(x+3)(x﹣1).
由题意可知:a=﹣1.
∴抛物线的解析式为y=﹣1(x+3)(x﹣1),即![]() ;
;
(2)如图所示:过点D作DE∥y轴,交AC于点E.
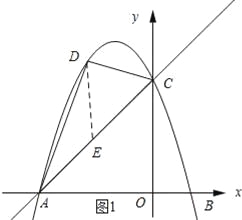
∵当x=0时,y=3,
∴C(0,3).
设直线AC的解析式为y=kx+3.
∵将A(﹣3,0)代入得:﹣3k+3=0,解得:k=1,
∴直线AC的解析式为y=x+3.
设点D的坐标为(x, ![]() ),则E点的坐标为(x,x+3).
),则E点的坐标为(x,x+3).
∴DE=![]() ﹣(x+3)=
﹣(x+3)=![]() .
.
∴△ADC的面积=![]() DEOA=
DEOA=![]() ×3×(
×3×(![]() )=
)=![]() .
.
∴当x=![]() 时,△ADC的面积有最大值.
时,△ADC的面积有最大值.
∴D![]() .
.
(3)如图2所示:
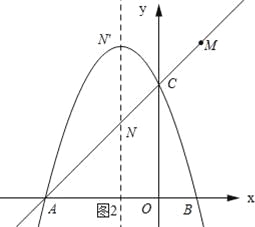
∵y=![]() =
=![]() ,
,
∴
∵点M与抛物线的顶点关于y轴对称,
∴M(1,4).
∵将x=1代入直线AC的解析式得y=4,
∴点M在直线AC上.
∵将x=﹣1代入直线AC的解析式得:y=2,
∴N(﹣1,2).
又∵当点N′与抛物线的顶点重合时,N′的坐标为(﹣1,4).
∴当2<t≤4时,直线MN与函数图象G有公共点.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A. 同旁内角相等,两直线平行
B. 对角线互相平分的四边形是平行四边形
C. 相等的两个角是对顶角
D. 圆内接四边形对角相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家今年刚成立的小型快递公司业务量逐月攀升,今年7月份和9月份完成投送的快递件数分别是20万件和24.2万件.若假设该公司每月投送的快递件数的增长率相同,则这家公司投送快递件数的月平均增长率为 ________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中:
(1)如图1,P,Q是BC边上的两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与点B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;
②小茹通过观察、实验提出猜想:在点P,Q运动的过程中,始终有PA=PM,小茹把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证明PA=PM,只需证△APM是等边三角形;
想法2:在BA上取一点N,使得BN=BP,要证明PA=PM,只需证△ANP≌△PCM;
想法3:将线段BP绕点B顺时针旋转60°,得到线段BK,要证PA=PM,只需证PA=CK,PM=CK…
请你参考上面的想法,帮助小茹证明PA=PM(一种方法即可).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com