

分析 (1)一个3×2的矩形可以是1个2×2和2个1×1或6个1×1的;
(2)一个5×2的矩形可以是2个2×2和2个1×1或1个2×2和6个1×1或10个1×1的;
(3)一个n×2的矩形用不同的方式分割后,小正方形都是1×1的小正方形的个数最多,分奇偶性讨论小正方形的个数最少的情况;
(4)由于要分成正方形,根据正方形的边长相等,分解的时候必须出现完全平方数,且边长不能大于原长方形的短边2,据此分解可得.
解答 解:(1)如图,
一个3×2的长方形用不同的方式分割后,小正方形的个数可以是3或6,
故答案为:3或6;
(2)如图,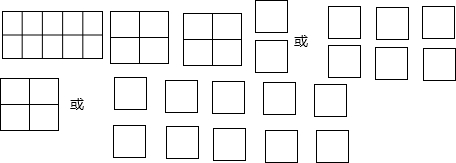
一个5×2的矩形用不同的方式分割后,小正方形的个数可以是4或7或10,
故答案为:4或7或10;
(3)一个n×2的矩形用不同的方式分割后,小正方形的个数最多是 2n;小正方形的个数最少是 ①n为偶数,有$\frac{n}{2}$个;②n为奇数,有$\frac{n+3}{2}$个;
故答案为:2n,n为偶数时有$\frac{n}{2}$个,n为奇数时有$\frac{n+3}{2}$个;
(4)∵18=9×2=9×1+4×1+1×5=9×1+1×9=4×3+1×6=4×2+1×10=4×1+1×14=1×18.
∴分割的正方形的个数可能是2个,1+1+5=7个,1+9=10个,3+6=9个,2+10=12个,1+14=15个,18个.
即分割所得小正方形的个数可能是2个,7个,10个,9个,12个,15个,18个,
故答案为:2或7或9或10或12或15或18
点评 本题考查了图形的规律型:图形的变化,关键是通过归纳与总结,得到其中的规律.正方形可以是1×1的或2×2的或3×3的.


科目:初中数学 来源: 题型:选择题
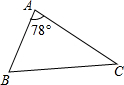 如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )| A. | 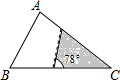 | B. |  | C. | 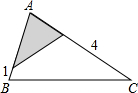 | D. | 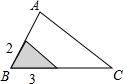 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点B,C,D在同一直线上,则∠1,∠2,∠3的大小关系是( )
如图,点B,C,D在同一直线上,则∠1,∠2,∠3的大小关系是( )| A. | ∠1<∠2<∠3 | B. | ∠1<∠3<∠2 | C. | ∠2<∠3<∠1 | D. | ∠3<∠2<∠1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
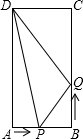 如图,在矩形ABCD中,AB=6cm,BC=12cm,点P沿边AB从点A向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向点C以2cm/s的速度移动,设点P、Q移动的时间为t s.问:
如图,在矩形ABCD中,AB=6cm,BC=12cm,点P沿边AB从点A向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向点C以2cm/s的速度移动,设点P、Q移动的时间为t s.问:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com