
 如图,四边形ABCD为平行四边形,E为BC的中点,连接AE并延长交DC的延长线于点F.
如图,四边形ABCD为平行四边形,E为BC的中点,连接AE并延长交DC的延长线于点F.分析 (1)由平行四边形的性质可得AB∥CF,则可求得∠BAE=∠CFE,结合题目条件可证得结论;
(2)由(1)可证得CF=DC,可得CH为△DFG的中位线,则可得CH∥AF,可证得CH⊥DG.
解答 (1)证明:
∵四边形ABCD为平行四边形,
∴AB∥DC,
∴∠BAE=∠CFE,
∵E为BC的中点,
∴BE=CE,
在△ABE和△FCE中
$\left\{\begin{array}{l}{∠BAE=∠CFE}\\{∠AEB=∠CEF}\\{BE=CE}\end{array}\right.$
∴△ABE≌△FCE(AAS);
(2)解:CH⊥DG.
理由如下:
由(1)可得△ABE≌△FCE,
∴AB=CF,
∵四边形ABCD为平行四边形,
∴AB=CD,
∴CF=CD,
∴C为FD的中点,
∵H为DG的中点,
∴CH为△DFG的中位线,
∴CH∥AE,
∵DG⊥AE,
∴∠DHC=∠DGF=90°,
∴DG⊥AE.
点评 本题主要考查平行四边形的性质,掌握平行四边形的对边平行且相等是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
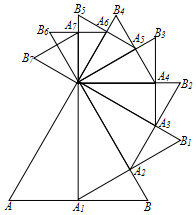 已知等边△OAB的边长为a,以AB边上的高OA1为边,按逆时针方向作等边△OA1B1,A1B1与OB相交于点A2;再以OA2为边按逆时针方向作等边△OA2B2,A2B2与OB1相交于点A3,按此作法进行下去,得到△OA3B3,△OA4B4,…,△OAnBn,(如图),则△OA6B6的周长是$\frac{81}{64}$a..
已知等边△OAB的边长为a,以AB边上的高OA1为边,按逆时针方向作等边△OA1B1,A1B1与OB相交于点A2;再以OA2为边按逆时针方向作等边△OA2B2,A2B2与OB1相交于点A3,按此作法进行下去,得到△OA3B3,△OA4B4,…,△OAnBn,(如图),则△OA6B6的周长是$\frac{81}{64}$a..查看答案和解析>>
科目:初中数学 来源: 题型:解答题
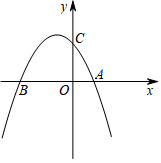 如图,抛物线y=ax2-x+4与x轴交于点A、B,B点的坐标为(-4,0),与y轴交于点C.
如图,抛物线y=ax2-x+4与x轴交于点A、B,B点的坐标为(-4,0),与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某体育场看台的坡面AB与地面的夹角是37°,看台最高点B到地面的垂直距离BC为2.4米,看台正前方有一垂直于地面的旗杆DE,在B点用测角仪测得旗杆的最高点E的仰角为33°,已知测角仪BF的高度为1.2米,看台最低点A与旗杆底端D之间的距离为15米(C,A,D在同一条直线上).
某体育场看台的坡面AB与地面的夹角是37°,看台最高点B到地面的垂直距离BC为2.4米,看台正前方有一垂直于地面的旗杆DE,在B点用测角仪测得旗杆的最高点E的仰角为33°,已知测角仪BF的高度为1.2米,看台最低点A与旗杆底端D之间的距离为15米(C,A,D在同一条直线上).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
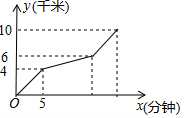 如图,小磊老师从甲地去往10千米的乙地,开始以一定的速度行驶,之后由于道路维修,速度变为原来的四分之一,过了维修道路后又变为原来的速度到达乙地.设小磊老师行驶的时间为x(分钟),行驶的路程为y(千米),图中的折线表示y与x之间的函数关系,则小磊老师从甲地到达乙地所用的时间是( )
如图,小磊老师从甲地去往10千米的乙地,开始以一定的速度行驶,之后由于道路维修,速度变为原来的四分之一,过了维修道路后又变为原来的速度到达乙地.设小磊老师行驶的时间为x(分钟),行驶的路程为y(千米),图中的折线表示y与x之间的函数关系,则小磊老师从甲地到达乙地所用的时间是( )| A. | 15分钟 | B. | 20分钟 | C. | 25分钟 | D. | 30分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=ax+b与x轴交于A,与y轴交于B,与双曲线y=$\frac{k}{x}$交于点C,D,OA=2OB=2.△OAB与△OAD的面积相等.
如图,直线y=ax+b与x轴交于A,与y轴交于B,与双曲线y=$\frac{k}{x}$交于点C,D,OA=2OB=2.△OAB与△OAD的面积相等.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知,A市到B市的路程为260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回A市,同时甲车以原来1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车所用时间x(小时)之间的函数图象,下列四种说法:
已知,A市到B市的路程为260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回A市,同时甲车以原来1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车所用时间x(小时)之间的函数图象,下列四种说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 496×105 | B. | 1 496×108 | C. | 1.496×105 | D. | 1.496×108 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com