

分析 (1)用10吨~15吨的用户除以所占的百分比,计算即可得解;
(2)用总户数减去其它四组的户数,计算求出15吨~20吨的用户数,然后补全直方图即可;用“25吨~30吨”所占的百分比乘以360°计算即可得解;
(3)用享受基本价格的用户数所占的百分比乘以7万,计算即可.
解答 解:(1)10÷10%=100(户);
答:此次调查抽取了100户的用水量数据,即样本容量是100.
故答案是:100;
(2)“15吨-20吨”部分的户数为100-(10+38+24+8)=20(户),
补全图形如下:
$\frac{20}{100}$×360°=72°;
(3)$\frac{10+20+38}{100}$×7=4.76(万户).
答:该地20万用户中约有4.76万户居民的用水全部享受基本价格.
点评 本题考查读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 型号 | 进价(元/只) | 售价(元/只) |
| A型 | 12 | 18 |
| B型 | 15 | 23 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
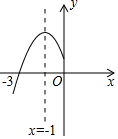 已知二次函数y=ax2+bx+c的图象如下,则一次函数y=ax-2b与反比例函数y=$\frac{c}{x}$在同一平面直角坐标系中的图象大致是( )
已知二次函数y=ax2+bx+c的图象如下,则一次函数y=ax-2b与反比例函数y=$\frac{c}{x}$在同一平面直角坐标系中的图象大致是( )| A. |  | B. | 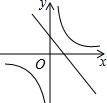 | C. |  | D. | 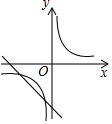 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
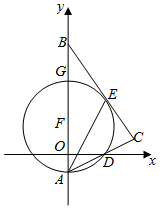 如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,AE平分∠BAC交边BC于点E,经过点A、D、E的圆的圆心F恰好在y轴上,⊙F与y轴相交于另一点G.
如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,AE平分∠BAC交边BC于点E,经过点A、D、E的圆的圆心F恰好在y轴上,⊙F与y轴相交于另一点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com