
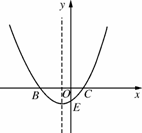
如图3415,已知抛物线y= (x-2)(x+a)(a>0)与x轴交于点B,C,与y轴交于点E,且点B在点C的左侧.
(x-2)(x+a)(a>0)与x轴交于点B,C,与y轴交于点E,且点B在点C的左侧.
(1)若抛物线过点M(-2,-2),求实数a的值;
(2)在(1)的条件下,解答下列问题;
①求出△BCE的面积;
②在抛物线的对称轴上找一点H,使CH+EH的值最小,直接写出点H的坐标.
解:(1)将M(-2,-2)代入抛物线解析式,得
-2= (-2-2)(-2+a),
(-2-2)(-2+a),
解得a=4.
(2)①由(1),得y= (x-2)(x+4),
(x-2)(x+4),
当y=0时,得0=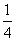 (x-2)(x+4),
(x-2)(x+4),
解得x1=2,x2=-4.
∵点B在点C的左侧,∴B(-4,0),C(2,0).
当x=0时,得y=-2,即E(0,-2).
∴S△BCE= ×6×2=6.
×6×2=6.
②由抛物线解析式y=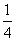 (x-2)(x+4),得对称轴为直线x=-1,
(x-2)(x+4),得对称轴为直线x=-1,
根据C与B关于抛物线对称轴x=-1对称,连接BE,与对称轴交于点H,即为所求.
设直线BE的解析式为y=kx+b,
将B(-4,0)与E(0,-2)代入,得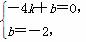
解得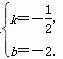 ∴直线BE的解析式为y=-
∴直线BE的解析式为y=- x-2.
x-2.
将x=-1代入,得y= -2=-
-2=-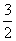 ,
,
则点H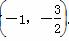 .
.


科目:初中数学 来源: 题型:
如图3311,菱形OABC的顶点C的坐标为(3,4).顶点A在x轴的正半轴上,反比例函数y=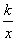 (x>0)的图象经过顶点B,则k的值为( )
(x>0)的图象经过顶点B,则k的值为( )
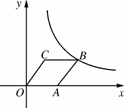
图3311
A.12 B.20 C.24 D.32
查看答案和解析>>
科目:初中数学 来源: 题型:
如图6224,已知:CD为一幢3米高的温室,其南面窗户的底框G距地面1米,CD在地面上留下的最大影长CF为2米,现欲在距C点7米的正南方A点处建一幢12米高的楼房AB(设A,C,F在同一水平线上).
(1)按比例较精确地作出高楼AB及它的最大影长AE;
(2)问若大楼AB建成后是否影响温室CD的采光,试说明理由.

图6224
查看答案和解析>>
科目:初中数学 来源: 题型:
某数学活动小组在作三角形的拓展图形,研究其性质时,经历了如下过程:
[操作发现]
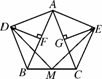
在等腰三角形ABC中,AB=AC,分别以AB和AC为斜边,向△ABC的外侧作等腰直角三角形,如图4247(1),其中DF⊥AB于点F,EG⊥AC于点G,M是BC的中点,连接MD和ME,则下列结论:①AF=AG= AB;②MD=ME;③整个图形是轴对称图形;④∠DAB=∠DMB.其中正确的是____________(填序号即可).
AB;②MD=ME;③整个图形是轴对称图形;④∠DAB=∠DMB.其中正确的是____________(填序号即可).
[数学思考]
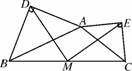
在任意△ABC中,分别以AB和AC为斜边,向△ABC的外侧作等腰直角三角形,如图4247(2),M是BC的中点,连接MD和ME,则MD和ME具有怎样的数量和位置关系?请给出证明过程.
[类比探索]
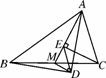
在任意△ABC中,仍分别以AB和AC为斜边,向△ABC的内侧作等腰直角三角形,如图4247(3),M是BC的中点,连接MD和ME,试判断△MED的形状.
答:____________________.
(1) (2) (3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com