
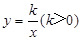 在第一象限图象上的一点,已知△P1O A1为等边三角形,点A1的坐标为(2,0).
在第一象限图象上的一点,已知△P1O A1为等边三角形,点A1的坐标为(2,0).
 );(2)
);(2) ;(3)(
;(3)( ,0).
,0). (k>0)图象上的一点,利用待定系数法求出此反比例函数的解析式;
(k>0)图象上的一点,利用待定系数法求出此反比例函数的解析式; );
); (
( >0)图象上,∴
>0)图象上,∴ ,
, ,
, ;
;
 a,P2H= P2 A1sin∠P2A1H=a·sin600=
a,P2H= P2 A1sin∠P2A1H=a·sin600= ,
, a,
a, ).
).  图象上,∴
图象上,∴ =
= ,
,  ,解得:
,解得: ,
, (舍去)
(舍去) ,∴A2(
,∴A2( ,0)
,0)

科目:初中数学 来源:不详 题型:解答题
 在第一象限内的交点.
在第一象限内的交点. 的坐标及
的坐标及 的值;
的值; 轴上确定一点
轴上确定一点 ,使
,使 ,求出点
,求出点 的坐标.
的坐标.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 (x>0)经过D点,交BC的延长线于E点,且OB•AC=160,有下列四个结论:①菱形OABC的面积为80; ②E点的坐标是(4,8);③双曲线的解析式为y=
(x>0)经过D点,交BC的延长线于E点,且OB•AC=160,有下列四个结论:①菱形OABC的面积为80; ②E点的坐标是(4,8);③双曲线的解析式为y=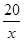 (x>0); ④
(x>0); ④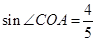 ,其中正确的结论有( )个。
,其中正确的结论有( )个。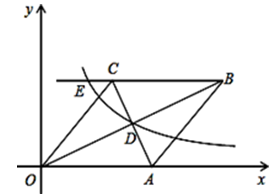
| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 的图象,如图所示,则
的图象,如图所示,则
| A.a>0,b>0,c>0 | B.a<0,b<0,c<0 |
| C.a<0,b>0,c>0 | D.a<0,b<0,c>0 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
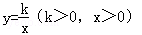 上的两点,BC∥x轴,交y轴于C,动点P从坐标原点O出发,沿O→A→B→C匀速运动,终点为C,过运动路线上任意一点P作PM⊥x轴于M,PN⊥y轴于N,设四边形OMPN的面积为S,P点运动的时间为t,则S关于t的函数图象大致是( )
上的两点,BC∥x轴,交y轴于C,动点P从坐标原点O出发,沿O→A→B→C匀速运动,终点为C,过运动路线上任意一点P作PM⊥x轴于M,PN⊥y轴于N,设四边形OMPN的面积为S,P点运动的时间为t,则S关于t的函数图象大致是( )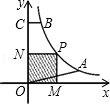
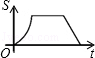 B
B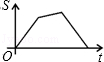 C
C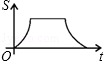 D
D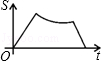
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
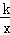 在第二象限的交点,AB⊥OA交x轴于点B,△AOB的面积为4,则k的值是_____________.
在第二象限的交点,AB⊥OA交x轴于点B,△AOB的面积为4,则k的值是_____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com