
 如图所示,一个圆柱形无盖的糖罐,高18cm,底面半径5cm,在外侧距下底1cm的点S处有一只蚂蚁,与蚂蚁正对的糖罐外侧距上口1cm处有一粒糖F,这只蚂蚁吃这粒糖至少要爬多少路程?(保留两位小数)
如图所示,一个圆柱形无盖的糖罐,高18cm,底面半径5cm,在外侧距下底1cm的点S处有一只蚂蚁,与蚂蚁正对的糖罐外侧距上口1cm处有一粒糖F,这只蚂蚁吃这粒糖至少要爬多少路程?(保留两位小数)科目:初中数学 来源: 题型:
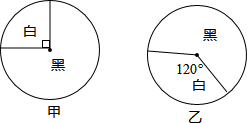 游戏组织者用如图所示的甲,乙两个转盘设计了一个游戏,规定:游戏参与者交1元钱可以分别转动甲,乙两个转盘各一次,若转盘停止时两指针的指向为下表中的组合:
游戏组织者用如图所示的甲,乙两个转盘设计了一个游戏,规定:游戏参与者交1元钱可以分别转动甲,乙两个转盘各一次,若转盘停止时两指针的指向为下表中的组合:| 两转盘颜色 (甲、乙) | (白,白) | (白,黑) | (黑,白) | (黑,黑) |
| 中奖金额(元) | 5 | 1 | 1 | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com