Question

8．如图，边OA，OC分别在x轴、y轴的正半轴上，OA∥BC，D是BC上一点，BD=$\frac{1}{4}OA=\sqrt{2}$，AB=3，∠OAB=45°，E，F分别是线段OA，AB上的两个动点，且始终保持∠DEF=45°，若△AEF为等腰三角形，则OE的长为$\frac{3\sqrt{2}}{2}$或3$\sqrt{2}$或3．

Answer 1

分析 因为△AEF为等腰三角形，所以要分三种情况进行讨论：①当EF=AF时，如图1，根据△AGB是直角三角形及斜边AB=3可求AG的长，即BG的长，从而求出AE的长，相减即可得出OE；
②当EF=AE时，如图2，AE=BD=$\sqrt{2}$，则OE=OA-AE即可；
③当AE=AF时，如图3，证明△ODE是等腰三角形，再求OD的长，就是OE的长．

解答 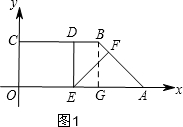解：当△AEF为等腰三角形，存在3种情况：
①当EF=AF时，如图1，过点B作BG⊥x轴于G，则△AGB是直角三角形，
∵BD=$\frac{1}{4}OA=\sqrt{2}$，
∴OA=4$\sqrt{2}$，
∵∠OAB=45°，
∴△AEF是等腰直角三角形，
∵∠DEF=45°，
∴∠DEA=90°，
则四边形DEGB是平行四边形，
∵AB=3，
∴AG=BG=$\frac{3\sqrt{2}}{2}$，
∴AE=AG+EG=$\frac{3\sqrt{2}}{2}$+BD=$\frac{3\sqrt{2}}{2}$+$\sqrt{2}$=$\frac{5\sqrt{2}}{2}$，
∴OE=OA-AE=4$\sqrt{2}$-$\frac{5\sqrt{2}}{2}$=$\frac{3\sqrt{2}}{2}$；
②当EF=AE时，如图2，
∵∠OAB=45°，
∴∠EFA=∠OAB=45°，
∴∠FEA=90°，
∵∠DEF=45°，
∴∠DEO=180°-90°-45°=45°，
∴∠DEO=∠OAB，
∴DE∥AB，
∵BC∥OA，
∴四边形DEAB是平行四边形，
∴AE=BD=$\sqrt{2}$，
∴OE=4$\sqrt{2}$-$\sqrt{2}$=3$\sqrt{2}$；
③当AE=AF时，如图3，
∵∠OAB=45°，
∴∠FEA=67.5°，
∵∠DEF=45°，
∴∠OED=180°-45°-67.5°=67.5°，
由（1）得：AG=BG=$\frac{3\sqrt{2}}{2}$，
∴CD=OA-AG-BD=4$\sqrt{2}$-$\frac{3\sqrt{2}}{2}$-$\sqrt{2}$=$\frac{3\sqrt{2}}{2}$，
∴CD=OC=$\frac{3\sqrt{2}}{2}$，
∴△COD是等腰直角三角形，则OD=$\sqrt{2}$CD=3，
∴∠COD=45°，
∴∠DOE=45°，
∴∠ODE=180°-45°-67.5°=67.5°，
∴∠ODE=∠OED，
∴OD=OE=3
综上所述：OE=$\frac{3\sqrt{2}}{2}$或3$\sqrt{2}$或3．

点评 本题是等腰三角形的动点问题，考查了等腰三角形及等腰直角三角形的性质及判定，当三点构成等腰三角形时，要分三种情况讨论，与坐标、图形相结合，利用线段的和与差求线段的长．