
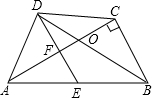
 在四边形ABCD中,BD平分∠ABC,E为AB的中点,DE∥CB,∠ACB=90°,下面的结论中,正确的有①③④.①△BDE为等腰三角形,②∠AED=∠AOD,③AO•OC=DO•OB,④∠CAB=30°时,四边形BCDE为菱形.
在四边形ABCD中,BD平分∠ABC,E为AB的中点,DE∥CB,∠ACB=90°,下面的结论中,正确的有①③④.①△BDE为等腰三角形,②∠AED=∠AOD,③AO•OC=DO•OB,④∠CAB=30°时,四边形BCDE为菱形. 分析 ①正确.可以通过证明∠EDB=∠EBD即可.
②错误.用反证法证明,推出不可能即可解决问题.
③正确.只要证明△AOD∽△BOC即可解决问题.
④正确.只要证明四边形BCDE是平行四边形,再证明ED=EB即可解决问题.
解答 解: ∵DE∥CB,
∵DE∥CB,
∴∠EDB=∠CBD,
∵∠CBD=∠DBE,
∴∠EDB=∠EBD,
∴ED=EB,
∴△BDE是等腰三角形,故①正确,
∵AE=EB=ED,
∴△ADB是直角三角形,
∴∠ADB=90°,
∵∠ACB=90°,
∴∠ADO=∠OCB,∵∠AOD=∠BOC,
∴△AOD∽△BOC,
∴$\frac{OD}{OC}$=$\frac{OA}{OB}$,
∴AO•OC=DO•OB,故③正确,
当∠CAB=30°时,易证BC=$\frac{1}{2}$AB=DE,∵DE∥BC,
∴四边形BCDE是平行四边形,∵ED=EB,
∴四边形BCDE是菱形,故④正确,
不妨设∠AED=∠AOD,则易证∠EAF=∠FDO=∠EBD=∠CBD,可得∠CAB=30°,显然假设错误,故②错误,
故答案为①③④
点评 本题考查平行四边形的判定和性质、菱形的判定、等腰三角形的性质、相似三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
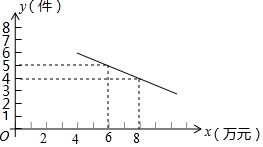 某公司销售某一种新型通讯产品,已知每件产品的进价为4万元,每月销售该种产品的总开支(不含进价)总计11万元.在销售过程中发现,月销售量y(件)与销售单价x (万元)之间存在着如图所示的一次函数关系.
某公司销售某一种新型通讯产品,已知每件产品的进价为4万元,每月销售该种产品的总开支(不含进价)总计11万元.在销售过程中发现,月销售量y(件)与销售单价x (万元)之间存在着如图所示的一次函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
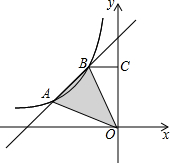 如图,直线y=x+4与双曲线y=$\frac{k}{x}$(x<0)交于点A、B,过点B向y轴作垂线,垂足为C,若BC=$\frac{1}{2}$AB,△AOB的面积为3,则k值为-3$\sqrt{2}$+$\frac{9}{8}$.
如图,直线y=x+4与双曲线y=$\frac{k}{x}$(x<0)交于点A、B,过点B向y轴作垂线,垂足为C,若BC=$\frac{1}{2}$AB,△AOB的面积为3,则k值为-3$\sqrt{2}$+$\frac{9}{8}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com