
(本题满分10分)在平行四边形ABCD中,AB=10,∠ABC=60°,以AB为直径作⊙O,边CD切⊙O于点E.

1.⑴求圆心O到CD的距离;
2.⑵求DE的长;
3.⑶求由弧AE、线段AD、DE所围成的阴影部分的面积.
(结果保留π和根号)
1.(1)连接OE.∵CD切⊙O于点E,
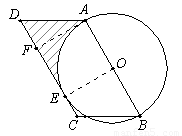
∴OE⊥CD.则OE的长度就是圆心O到CD的距离.
∵AB是⊙O的直径,OE是⊙O的半径,
∴OE=AB=5.即圆心⊙到CD的距离是5.
2.(2)过点A作AF⊥CD,垂足为F.∵四边形ABCD是平行四边形,∴∠B=∠D=60°,AB∥CD.∵AB∥CD,OE⊥CD,AF⊥CD,∴OA=OE=AF=EF=5.在Rt△ADF中,∠D=60°,AF=5,∴DF=,∴DE=5+.
3.(3)在直角梯形AOED中,OE=5,OA=5,DE=5+,
∴S梯形AOED=×(5+5+)×5=25+.∵∠AOE=90°,∴S扇形OAE=×π×52=π.∴S阴影= S梯形AOED- S扇形OAE=25+- π.即由弧AE、线段AD、DE所围成的阴影部分的面积为25+-π.
【解析】略


科目:初中数学 来源: 题型:
(本题满分10分)在平面直角坐标系中,点P从原点O出发,每次向上平移2个单位长度或向右平移1个单位长度.
(1)实验操作: 在平面直角坐标系中描出点P从点O出发,平移1次后,2次后,3次后可能到达的点,并把相应点的坐标填写在表格中:
(2)观察发现:任一次平移,点P可能到达的点在我们学过的一种函数的图象上,如:平移1次后在函数 的图象上;平移2次后在函数 的图象上……由此我们知道,平移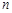 次后在函数 的图象上.(请填写相应的解析式)
次后在函数 的图象上.(请填写相应的解析式)
(3)探索运用:点P从点O出发经过![]() 次平移后,到达直线
次平移后,到达直线![]() 上的点Q,且平移的路径长不小于50,不超过56,求点Q的坐标.
上的点Q,且平移的路径长不小于50,不超过56,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(海南卷)数学解析版 题型:解答题
(本题满分10分)
在直角三角形ABC中,∠C=90°,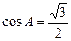 ,∠B的平分线BD交AC于D,BD=16.求AB的长.
,∠B的平分线BD交AC于D,BD=16.求AB的长.
查看答案和解析>>
科目:初中数学 来源:2010年高级中等学校招生全国统一考试数学卷(山东莱芜) 题型:解答题
(本题满分10分) 在 ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.
在 ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.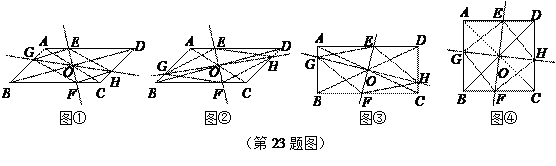
(1)如图①,试判断四边形EGFH的形状,并说明理由;
(2)如图②,当EF⊥GH时,四边形EGFH的形状是 ;
(3)如图③,在(2)的条件下,若AC=BD,四边形EGFH的形状是 ;
(4)如图④,在(3)的条件下,若AC⊥BD,试判断四边形EGFH的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源:2013届海南省三亚市七年级下学期期末考试数学 题型:解答题
(本题满分10分)
在直角三角形ABC中,∠C=90°,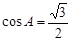 ,∠B的平分线BD交AC于D,BD=16.求AB的长.
,∠B的平分线BD交AC于D,BD=16.求AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com