


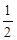 •x•
•x• x=
x=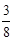 x2,(0<x≤8);(2) 当x=
x2,(0<x≤8);(2) 当x=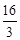 时,y有最大值,最大值为8.
时,y有最大值,最大值为8.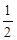 •x•
•x• x=
x=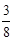 x2,根据二次函数的性质得到x=4,y的最大值为6;当4<x≤8时,PM与PN分别交BC于E、F,y=S梯形MEFN=S△PMN-S△PEF,利用矩形的性质可表示出PN=AM=x;再由平行四边形BFNM的性质解得FN=8-x,PF=2x-8,则可利用相似三角形Rt△PEF∽Rt△ABC的性质求得S△PEF值;然后写出y与x的解析式,再根据二次函数的性质求出y的最大值,最后综合两种情况即可.
x2,根据二次函数的性质得到x=4,y的最大值为6;当4<x≤8时,PM与PN分别交BC于E、F,y=S梯形MEFN=S△PMN-S△PEF,利用矩形的性质可表示出PN=AM=x;再由平行四边形BFNM的性质解得FN=8-x,PF=2x-8,则可利用相似三角形Rt△PEF∽Rt△ABC的性质求得S△PEF值;然后写出y与x的解析式,再根据二次函数的性质求出y的最大值,最后综合两种情况即可.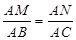 ,
,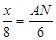 ,解得AN=
,解得AN= x,
x,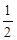 •x•
•x• x=
x=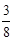 x2,
x2,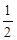 •x•
•x• x=
x=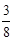 x2,(0<x≤8);
x2,(0<x≤8);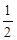 •x•
•x• x=
x=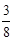 x2,此时x=4,y的最大值为6;
x2,此时x=4,y的最大值为6;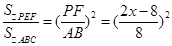 ,
,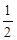 ×8×6=24,
×8×6=24,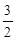 (x-4)2,
(x-4)2,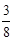 x2-
x2-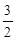 (x-4)2
(x-4)2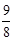 x2+12x-24,
x2+12x-24,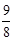 (x-
(x-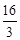 )2+8(4<x≤8),
)2+8(4<x≤8),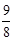 <0,
<0,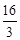 时,y有最大值,最大值为8,
时,y有最大值,最大值为8,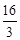 时,y有最大值,最大值为8.
时,y有最大值,最大值为8.

科目:初中数学 来源:不详 题型:解答题
 ).则每户平均集资的资金在150元的基础上减少了
).则每户平均集资的资金在150元的基础上减少了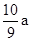 %,求a的值.
%,求a的值.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
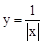 的图象在第一象限的一支曲线上有一点A(a,c),点B(b,c+1)在该函数图象的另外一支上,则关于一元二次方程ax2+bx+c = 0的两根x1,x2判断正确的是( )
的图象在第一象限的一支曲线上有一点A(a,c),点B(b,c+1)在该函数图象的另外一支上,则关于一元二次方程ax2+bx+c = 0的两根x1,x2判断正确的是( )| A.x1 + x2 >1,x1·x2 > 0 |
| B.x1 + x2 < 0,x1·x2 > 0 |
| C.0 < x1 + x2 < 1,x1·x2 > 0 |
| D.x1 + x2与x1·x2 的符号都不确定 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.没有实数根 | B.有两个相等的实数根 |
| C.有两个不相等的实数根 | D.无法判断 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com