
【题目】如图,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下列结论①△ODC是等边三角形;②BC=2AB;③∠AOE=135°;④S△AOE=S△COE 其中正确的结论的序号是__________
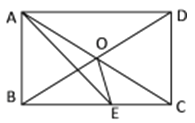
【答案】①③④
【解析】∵矩形ABCD中,AE平分∠BAD, ∴∠BAE=45°, ∵∠CAE=15°, ∴∠BAO=∠BAE+∠CAE=45°+15°=60°,又∵矩形中OA=OB=OC=OD, ∴△AOB是等边三角形,∴∠AOB=∠COD=60°, ∴△ODC是等边三角形,故①正确;由等边三角形的性质,AB=OA, ∴AC=2AB,由垂线段最短BC<AC, ∴BC<2AB,故②错误;∵∠BAE=45°, ∠ABE=90°, ∴△ABE是等腰直角三角形,∴AB=BE,BO=BE, ∵∠COB=180°-60°=120°, ∴∠BOE=![]() (180°-30°)=75°,
(180°-30°)=75°,
∴∠AOE=∠AOB+∠BOE=60°+75°=135°,故③正确;∵△AOE和△COE的底边AO=CO,点E到AC的距离相等,∴![]() ,故④正确;综上所述,正确的结论是①③④.
,故④正确;综上所述,正确的结论是①③④.
点睛:本题考查了矩形的性质,等边三角形的判定与性质,等腰三角形的性质,垂线段最短,等底等高的三角形的面积相等,综合题,但难度不大,熟记性质并准确识图理清图中各角度之间的关系是解题的关键.


科目:初中数学 来源: 题型:
【题目】若∠A和∠B的两边分别平行,且∠A比∠B的2倍少30°,则∠B的度数为( )
A. 30° B. 70° C. 30°或70° D. 100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=CD=6cm,BC=10cm,点P从点B出发,以2cm/秒的速度沿BC向点C运动,设点P的运动时间为t秒:
(1)PC=______cm.(用t的代数式表示)
(2)当t为何值时,△ABP≌△DCP?
(3)当点P从点B开始运动,同时,点Q从点C出发,以v cm/秒的速度沿CD向点D运动,是否存在这样v的值,使得△ABP与△PQC全等?若存在,请求出v的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一鞋店试销一种新款女鞋,试销期间卖出情况如表:
型号 | 220 | 225 | 230 | 235 | 240 | 245 | 250 |
数量(双) | 3 | 5 | 10 | 15 | 8 | 3 | 2 |
对于这个鞋店的经理来说最关心哪种型号的鞋畅销,则下列统计量对鞋店经理来说最有意义的是( )
A. 平均数B. 众数C. 中位数D. 方差
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com