
【题目】某水果基地计划装运甲、乙、丙三种水果到外地销售(每辆汽车规定满载,并且只装一种水果).如表为装运甲、乙、丙三种水果的重量及利润.
甲 | 乙 | 丙 | |
每辆汽车能装的数量(吨) | 4 | 2 | 3 |
每吨水果可获利润(千元) | 5 | 7 | 4 |
(1)用8辆汽车装运乙、丙两种水果共22吨到A地销售,问装运乙、丙两种水果的汽车各多少辆?
(2)水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售(每种水果不少于一车),假设装运甲水果的汽车为m辆,则装运乙、丙两种水果的汽车各多少辆?(结果用m表示)
(3)在(2)问的基础上,如何安排装运可使水果基地获得最大利润?最大利润是多少?
【答案】
(1)解:设装运乙、丙水果的车分别为x辆,y辆,得:
![]() ,
,
解得: ![]() .
.
答:装运乙种水果的车有2辆、丙种水果的汽车有6辆
(2)解:设装运乙、丙水果的车分别为a辆,b辆,得:
![]() ,
,
解得 ![]() .
.
答:装运乙种水果的汽车是(m﹣12)辆,丙种水果的汽车是(32﹣2m)辆
(3)解:设总利润为w千元,
w=5×4m+7×2(m﹣12)+4×3(32﹣2m)=10m+216.
∵ 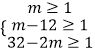 ,
,
∴13≤m≤15.5,
∵m为正整数,
∴m=13,14,15,
在w=10m+216中,w随x的增大而增大,
∴当m=15时,W最大=366(千元),
答:当运甲水果的车15辆,运乙水果的车3辆,运丙水果的车2辆,利润最大,最大利润为366千元
【解析】(1)根据“8辆汽车装运乙、丙两种水果共22吨到A地销售”列出方程组,即可解答;(2)设装运乙、丙水果的车分别为a辆,b辆,列出方程组 ![]() ,即可解答;(3)设总利润为w千元,表示出w=10m+216.列出不等式组
,即可解答;(3)设总利润为w千元,表示出w=10m+216.列出不等式组 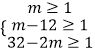 ,确定m的取值范围13≤m≤15.5,结合一次函数的性质,即可解答.
,确定m的取值范围13≤m≤15.5,结合一次函数的性质,即可解答.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为F,G,若正方形ABCD的周长是40cm.
(1)求证:四边形BFEG是矩形;
(2)求四边形EFBG的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班数学课外活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处测得树顶端D的仰角为60°,已知A点的高度AB为2米,台阶AC的坡度i=1:2,且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测倾器的高度忽略不计,结果保留根号) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点A,给出如下定义:若存在点B(不与点A重合,且直线AB不与坐标轴平行或重合),过点A作直线m∥x轴,过点B作直线n∥y轴,直线m,n相交于点C.当线段AC,BC的长度相等时,称点B为点A 的等距点,称三角形ABC的面积为点A的等距面积. 例如:如图,点A(2,1),点B(5,4),因为AC= BC=3,所以B为点A 的等距点,此时点A的等距面积为![]() .
.
(1)点A的坐标是(0,1),在点B1(-1,0),B2(2,3),B3(-1,-1)中,点A 的等距点为________________.
(2)点A的坐标是(-3,1),点A的等距点B在第三象限,
①若点B的坐标是![]() ,求此时点A的等距面积;
,求此时点A的等距面积;
②若点A的等距面积不小于![]() ,求此时点B的横坐标t的取值范围.
,求此时点B的横坐标t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课上,老师要求学生在5×5的正方形ABCD网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在格点上,而且三边与AB或AD都不平行.画四种图形,并直接写出其周长(所画图象相似的只算一种). 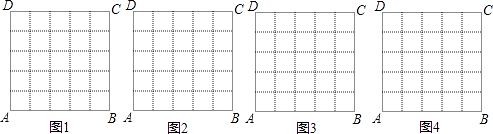
查看答案和解析>>
科目:初中数学 来源: 题型:
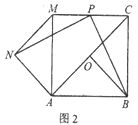
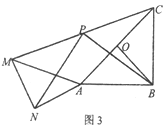
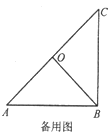
【题目】已知,△AOB中,AB=BC=2,∠ABC=90°,点O是线段AC的中点,连接OB,将△AOB绕点A逆时针旋转α度得到△ANM,连接CM,点P是线段CM的中点,连接PN、PB.
(1)如图1,当α=180°时,直接写出线段PN和PB之间的位置关系和数量关系;
(2)如图2,当α=90°时,探究线段PN和PB之间的位置关系和数量关系,并给出完整的证明过程;
(3)如图3,直接写出当△AOB在绕点A逆时针旋转的过程中,线段PN的最大值和最小值.
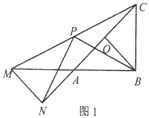
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,AD为等腰直角△ABC的高,点A和点C分别在正方形DEFG的边DG和DE上,连接BG,AE.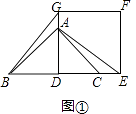
(1)求证:BG=AE;
(2)将正方形DEFG绕点D旋转,当线段EG经过点A时,(如图②所示)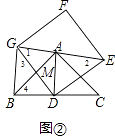
①求证:BG⊥GE;
②设DG与AB交于点M,若AG:AE=3:4,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,AC,BD是对角线。将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG。则下列结论:
①四边形AEGF是菱形 ②△AED≌△GED
③∠DFG=112.5° ④BC+FG=1.5
其中正确的结论是( )
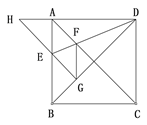
A. ①②③④ B. ①②③ C. ①② D. ②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com