
【题目】已知关于x的方程x2﹣(m+n+1)x+m(n≥0)的两个实数根为α、β,且α≤β.
(1)试用含α、β的代数式表示m和n;
(2)求证:α≤1≤β;
(3)若点P(α,β)在△ABC的三条边上运动,且△ABC顶点的坐标分别为A(1,2)、B(![]() ,1)、C(1,1),问是否存在点P,使m+n=
,1)、C(1,1),问是否存在点P,使m+n=![]() ?若存在,求出点P的坐标;若不存在,请说明理由.
?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)m=αβ,n=α+β﹣αβ﹣1;(2)详见解析;(3)详见解析.
【解析】分析:(1)、根据韦达定理即可得出答案;(2)、首先求出(1﹣α)(1﹣β)的值为-n,从而根据n的取值范围得出答案;(3)、先根据条件确定动点所在的边,然后再确定点的坐标.
详解:解:(1)∵α、β为方程x2﹣(m+n+1)x+m=0(n≥0)的两个实数根,
∴判别式△=(m+n+1)2﹣4n=(m+n﹣1)2+4n≥0,且α+β=m+n+1,αβ=m,
于是m=αβ,n=α+β﹣m﹣1=α+β﹣αβ﹣1;
(2)∵(1﹣α)(1﹣β)=1﹣(α+β)+αβ=﹣n≤0(n≥0),又α≤β,∴α≤1≤β;
(3)若使m+n成立,只需α+β=m+n+1=![]() ,
,
①当点M(α,β)在BC边上运动时,由B(![]() ,1),C(1,1),得
,1),C(1,1),得![]() ≤α≤1,β=1,
≤α≤1,β=1,
而α=![]() ﹣β=
﹣β=![]() ﹣1=
﹣1=![]() >1,故在BC边上存在满足条件的点,其坐标为(
>1,故在BC边上存在满足条件的点,其坐标为(![]() ,1)所以不符合题意舍去; 即在BC边上不存在满足条件的点
,1)所以不符合题意舍去; 即在BC边上不存在满足条件的点
②当点M(α,β)在AC边上运动时,由A(1,2),C(1,1),得α=1,1≤β≤2,
此时β=![]() ﹣α=
﹣α=![]() ﹣1=
﹣1=![]() ,又因为1<
,又因为1<![]() <2,故在AC边上存在满足条件的点,其坐标为(1,
<2,故在AC边上存在满足条件的点,其坐标为(1, ![]() );
);
③当点M(α,β)在AB边上运动时,由A(1,2),B(![]() ,1),得
,1),得![]() ≤α≤1,1≤β≤2,
≤α≤1,1≤β≤2,
由平面几何知识得,  ,于是β=2α,由
,于是β=2α,由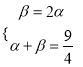 ,解得α=
,解得α=![]() ,β=
,β=![]() ,
,
又因为![]() <
<![]() <1,1<
<1,1<![]() <2,故在AB边上存在满足条件的点,其坐标为(
<2,故在AB边上存在满足条件的点,其坐标为(![]() ,
, ![]() ).
).
综上所述,当点M(α,β)在△ABC的三条边上运动时,存在点(1, ![]() )和点(
)和点(![]() ,
, ![]() ),使m+n=
),使m+n=![]() 成立.
成立.


科目:初中数学 来源: 题型:
【题目】有甲、乙两种糖果,原价分别为每千克a元和b元.根据调查,将两种糖果按甲种糖果x千克与乙种糖果y千克的比例混合,取得了较好的销售效果.现在糖果价格有了调整:甲种糖果单价下降15%,乙种糖果单价上涨20%,但按原比例混合的糖果单价恰好不变,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=x2+bx+c的图像与x 轴交于A、B两点,与y轴交于点C,OB=OC.点D在函数图像上,CD//x轴,且CD=2,直线l 是抛物线的对称轴,E是抛物线的顶点.
(1)求b、c 的值;
(2)如图①,连接BE,线段OC 上的点F 关于直线l 的对称点F′ 恰好在线段BE上,求点F的坐标;
(3)如图②,动点P在线段OB上,过点P 作x 轴的垂线分别与BC交于点M,与抛物线交于点N.试问:抛物线上是否存在点Q,使得△PQN与△APM的面积相等,且线段NQ的长度最小?如果存在,求出点Q的坐标;如果不存在,说明理由.

图 ① 图②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E.
(1)如图1,求证∠BAC=∠B+2∠E;
(2)如图2,过点A作AF⊥BC,垂足为点F,若∠DCE=2∠CAF,∠B=2∠E,求∠BAC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班级同学从学校出发去太阳岛研学旅行,一部分乘坐大客车先出发,余下的同学20min后乘坐小轿车沿同一路线出行,大客车中途停车等候5min,小轿车赶上来之后,大客车以出发时速度的![]() 继续行驶,小轿车保持原速度不变.小轿车司机因路线不熟错过了景点入口,在驶过景点入口6 km时,原路提速返回,恰好与大客车同时到达景点入口.两车距学校的路程S(单位:km)和行驶时间t(单位:min)之间的函数关系如图所示.
继续行驶,小轿车保持原速度不变.小轿车司机因路线不熟错过了景点入口,在驶过景点入口6 km时,原路提速返回,恰好与大客车同时到达景点入口.两车距学校的路程S(单位:km)和行驶时间t(单位:min)之间的函数关系如图所示.
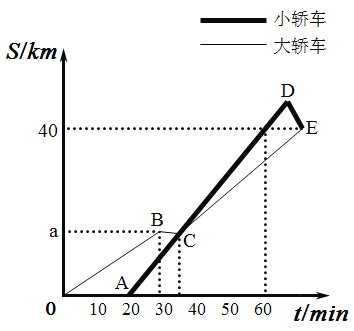
请结合图象解决下面问题:
(1)学校到景点的路程为________km,![]() ________;
________;
(2)在小轿车司机驶过景点入口时,大客车离景点入口还有多远?
(3)小轿车司机到达景点入口时发现本路段限速80 km/h,请你帮助小轿车司机计算折返时是否超速?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA=2,以点A为圆心,1为半径画⊙A与OA的延长线交于点C,过点A画OA的垂线,垂线与⊙A的一个交点为B,连接BC

(1)线段BC的长等于 ;
(2)请在图中按下列要求逐一操作,并回答问题:
①以点 为圆心,以线段 的长为半径画弧,与射线BA交于点D,使线段OD的长等于![]() ;
;
②连OD,在OD上画出点P,使OP得长等于![]() ,请写出画法,并说明理由.
,请写出画法,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,多项式的因式分解就是将一个多项式化成几个整式的积的形式.通过因式分解,我们常常将一个次数比较高的多项式转化成几个次数较低的整式的积,来达到降次化简的目的.这个思想可以引领我们解决很多相对复杂的代数问题.
例如:方程![]() 就可以这样来解:
就可以这样来解:
解:原方程可化为:![]()
所以![]() 或者
或者![]()
解方程![]() 得:
得:![]()
所以原方程的解:![]() ,
,![]()
根据你的理解,结合所学知识,解决以下问题:
(1)解方程:![]() ;
;
(2)已知![]() 的三边为4、x、y,请你判断代数式
的三边为4、x、y,请你判断代数式![]() 的值的符号.
的值的符号.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ABC=∠DCB,添加一个条件使△ABC≌△DCB,下列添加的条件不能使△ABC≌△DCB的是( )

A. ∠A=∠D B. AB=DC C. AC=DB D. OB=OC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com